On March 14 at 1:59pm, folks from all over the world celebrate “Pi Day” with games, activities, and pie-eating contests. Here are my best resources for showing kids how pi shows up in the real world and also how to learn about pi in a way that not only makes sense but isn’t flat boring.
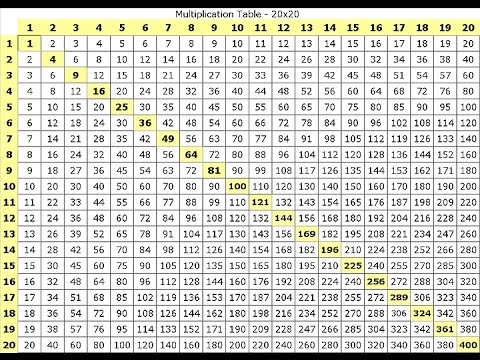
Pi (p) is a number slightly greater than 3 that shows up when you divide the circumference of a circle by its diameter, no matter what size the circle is. It also shows up in other shapes like spheres, ellipses, cylinders, and cones as well as unusual places like summation series, number theory, probability, bell curves, and the Fibonacci series.
I’ve prepared two different versions that you can access, and each comes with its own video. If this is your first time encountering “pi”, then start with the first one. Otherwise, jump in to the full version and have fun!
Please login or register to read the rest of this content.
Over the years, I’ve collected quite a stash of activity sheets and games for kids from other sources. I don’t know where they all came from, so please respect their copyright information on the sheet itself when you share with others.






 Everyone old enough to remember the Rubik’s Cube craze of the 1980s in the USA also remembers how it was near impossible to solve the thing! Originally created by a professor of architecture Erno Rubik, it was sold to a toy company in 1980 as the “Magic Cube”.
Everyone old enough to remember the Rubik’s Cube craze of the 1980s in the USA also remembers how it was near impossible to solve the thing! Originally created by a professor of architecture Erno Rubik, it was sold to a toy company in 1980 as the “Magic Cube”.

 Cryptarithms are a puzzle where the digits are replaced by letters or symbols. When the numbers are replaced by letters of the alphabet and it spells something readable, it’s called Alphametics.
Cryptarithms are a puzzle where the digits are replaced by letters or symbols. When the numbers are replaced by letters of the alphabet and it spells something readable, it’s called Alphametics.










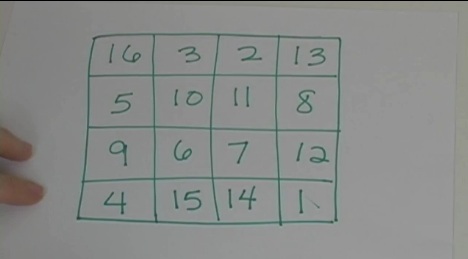
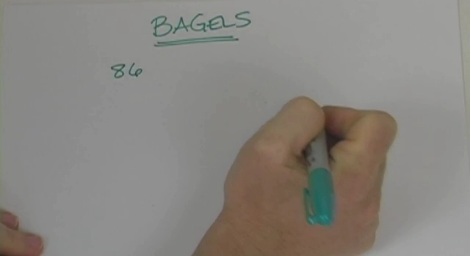















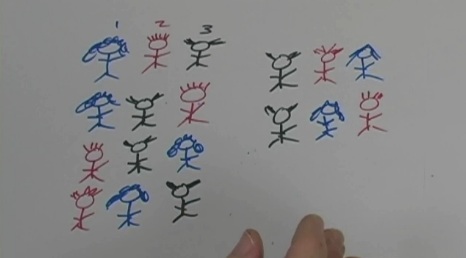



 If you've ever wanted to sneak a peek into my cabinet of educational games and books for kids, now is your chance. Use this list for gift ideas, boredom busters, and just plain family fun. Some of these games you can pick up at the store, and the rest are the home-made, print-it-out, cut-and-play variety that your kids will really learn from.
If you've ever wanted to sneak a peek into my cabinet of educational games and books for kids, now is your chance. Use this list for gift ideas, boredom busters, and just plain family fun. Some of these games you can pick up at the store, and the rest are the home-made, print-it-out, cut-and-play variety that your kids will really learn from. Math Games
Math Games
 Most resources that public school advisers suggest for gifted or bright kids are a ‘mile wide and an inch deep’ – they don’t really go into depth on any one area. After traveling to dozens of home school conventions for several years across the country and seeing what math options are out there, I searched for more options than what’s traditionally on the exhibit floor.
Most resources that public school advisers suggest for gifted or bright kids are a ‘mile wide and an inch deep’ – they don’t really go into depth on any one area. After traveling to dozens of home school conventions for several years across the country and seeing what math options are out there, I searched for more options than what’s traditionally on the exhibit floor.
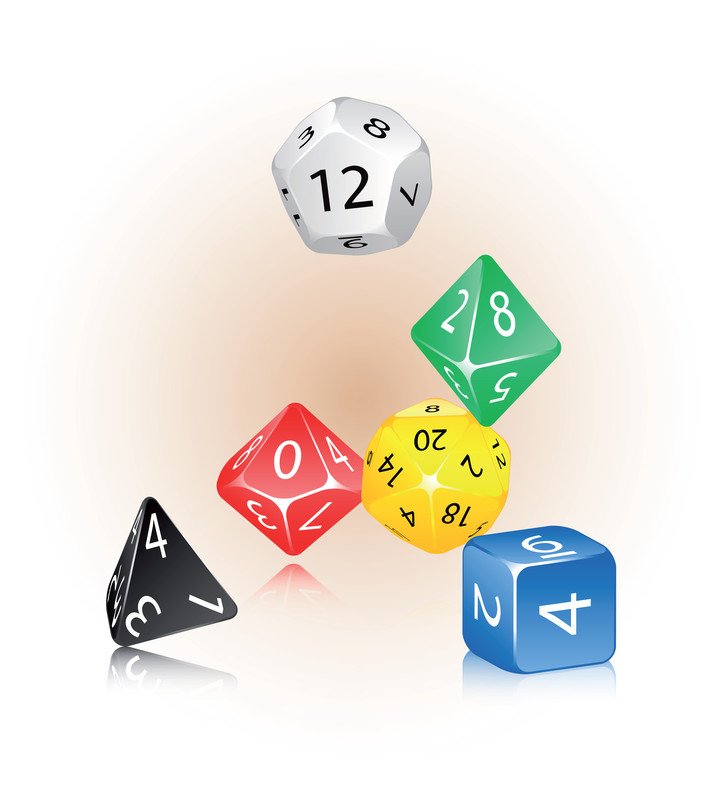

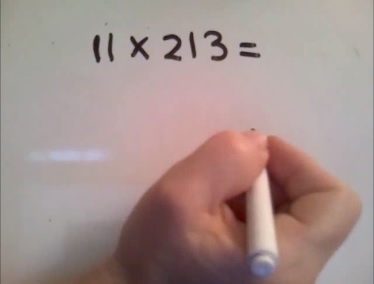




 One day, my kid asked me how a calculator comes up with its answers. That's a great question, I thought. How does a calculator do math?
One day, my kid asked me how a calculator comes up with its answers. That's a great question, I thought. How does a calculator do math?