Do you remember when I asked you “Who pushed you?” when you were riding in a car that took a sharp turn? Well, the answer has to do with centripetal force. Centripetal (translation = “center-seeking” ) is the force needed to keep an object following a curved path.
Remember how objects will travel in a straight line unless they bump into something or have another force acting on it like gravity, friction, or drag force? Imagine a car moving in a straight line at a constant speed. You’re inside the car, no seat belt, and the seat is slick enough for you to slide across easily. Now the car turns and drives again at constant speed but now on a circular path. When viewed from above the car, we see the car following a circle, and we see you wanting to keep moving in a straight line, but the car wall (door), moves into your path and exerts a force on you to keep you moving in a circle. The car door is pushing you into the circle.
According to Newton’s second law of motion, if you are experiencing an acceleration you must also be experiencing a net force (F=ma). The direction of the net force is in the same direction as the acceleration, so for the example with you inside the car, there’s an inward force acting on you (from the car door) keeping you moving in a circle.
If you have a bucket of water and you’re swinging it around your head, in order to keep a bucket of water swinging in a circle, the centripetal force can be felt in the tension experienced by the handle. Swinging an object around on a string will cause the rope to undergo tension (centripetal force), and if your rope isn’t strong enough, it will snap and break, sending the mass flying off in a tangential straight line until gravity and drag force pull the object to a stop.
This force is proportional to the square of the speed, meaning that the faster you swing the object, the higher the magnitude of the force will be.
Remember Newton’s First Law? The law of inertia? It states that objects in motion tend to stay in motion with the same speed and direction unless acted upon by an unbalanced/external force. Which means that objects naturally want to continue going their straight and merry way (like you did in a straight line when you were inside the car) until an unbalanced force causes it to turn speed up or stop. Can you see how an unbalanced force is required for objects to move in a circle? There has to be a force pushing on the object, keeping in on a circular path because otherwise, it’ll go off in a straight line!
Please
login or
register to read the rest of this content.


 If you watch the moon, you’d notice that it rises in the east and sets in the west. This direction is called ‘prograde motion’. The stars, sun, and moon all follow the same prograde motion, meaning that they all move across the sky in the same direction.
If you watch the moon, you’d notice that it rises in the east and sets in the west. This direction is called ‘prograde motion’. The stars, sun, and moon all follow the same prograde motion, meaning that they all move across the sky in the same direction.












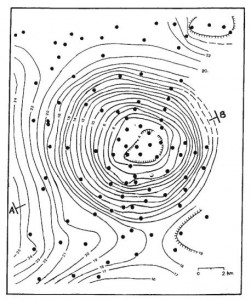 First, the crust is not uniform. There are lumps and clumps everywhere that vary the density add up to make small variations in the force of gravity that we can actually measure with objects in free-fall motion. It’s actually how scientists find pockets of oil in the earth. They measure the surface gravity and plot it out, and if there’s a large enough deviation, it means there’s something interesting underground.
First, the crust is not uniform. There are lumps and clumps everywhere that vary the density add up to make small variations in the force of gravity that we can actually measure with objects in free-fall motion. It’s actually how scientists find pockets of oil in the earth. They measure the surface gravity and plot it out, and if there’s a large enough deviation, it means there’s something interesting underground. Centrifugal (translation = “center-fleeing”) force has two different definitions, which causes even more confusion. The inertial centrifugal force is the most widely referred to, and is purely mathematical, having to do with calculating kinetic forces using reference frames, and is used with Newton’s laws of motion. It’s often referred to as the ‘fictitious force’.
Centrifugal (translation = “center-fleeing”) force has two different definitions, which causes even more confusion. The inertial centrifugal force is the most widely referred to, and is purely mathematical, having to do with calculating kinetic forces using reference frames, and is used with Newton’s laws of motion. It’s often referred to as the ‘fictitious force’. Imagine an arrow is shot from a bow and by the time it hits an apple it is traveling with 10 Joules of kinetic energy (kinetic energy is the energy of motion). What’s meant by kinetic energy is that when it hits something, it can do that much work on whatever is hit.
Imagine an arrow is shot from a bow and by the time it hits an apple it is traveling with 10 Joules of kinetic energy (kinetic energy is the energy of motion). What’s meant by kinetic energy is that when it hits something, it can do that much work on whatever is hit.