Johannes Kepler, a German mathematician and astronomer in the 1600s, was one of the key players of his time in astronomy. Among his best discoveries was the development of three laws of planetary orbits. He worked for Tycho Brahe, who had logged huge volumes of astronomical data, which was later passed onto to Kepler. Kepler took this information to design and develop his ideas about the movements of the planets around the Sun.
Kepler’s 1st Law states that planetary orbits about the Sun are not circles, but rather ellipses. The Sun lies at one of the foci of the ellipse.
Well, almost.
Newton’s Laws of Motion state that the Sun can’t be stationary, because the Sun is pulling on the planet just as hard as the planet is pulling on the Sun. They are yanking on each other. The planet will move more due to this pulling because it is less massive. The real trick to understanding this law is that both objects orbit around a common point that is the center of mass for both objects. If you’ve ever swung a heavy bag of oranges around in a circle, you know that you have to lean back a bit to balance yourself as you swing around and around. It’s the same principle, just on a smaller scale.
[am4show have=’p9;p58;’ guest_error=’Guest error message’ user_error=’User error message’ ]
In our solar system the Sun has 99.85% of the mass, so the center of mass between the Sun and any other object actually lies inside the Sun (although not at the center).
Kepler’s 2nd Law states that a line connecting the Sun and an orbiting planet will sweep out equal areas in for a given amount of time. The planet’s speed decreases the further from the Sun it is located (actually, the speed varies inversely with the square‐root of the distance, but you needn’t worry about that).
You can see this for yourself by tying a ball to the end of a string and whirl it around in a circle. After a few revolutions, let the string wind itself up around your finger. As the string length shortens, the ball speeds up. As the planet moves inward, the planet’s orbital speed increases.
Embedded in the second law are two very important laws: conservation of angular moment and conservation of energy. Although those laws might sound scary, they are not difficult to understand. Angular momentum is distance multiplied by mass multiplied by speed. The angular momentum for one case must be the same for the second case (otherwise it wouldn’t be conserved). As the planet moves in closer to the Sun, the distance decreases. The speed it orbits the Sun must increase because the mass doesn’t change. Just like you saw when you wound the ball around your finger.
Energy is the sum of both the kinetic (moving) energy and the potential energy (this is the “could” energy, as in a ball dropped from a tower has more potential energy than a ball on the ground, because it “could” move if released). For conservation of energy, as the planet’s distance from the Sun increases, so does the gravitational potential energy. Again, since the energy for the first case must equal the energy from the second case (that’s what conservation means), the kinetic energy must decrease in order to keep the total energy sum a constant value.
Kepler’s 3rd Law is an equation that relates the revolution period with the average orbit speed.
The important thing to note here is that mass was not originally in this equation. Newton came along shortly after and did add in the total mass of the system, which fixed the small error with the equation. This makes sense, as you might imagine a Sun twice the size would cause the Earth to orbit faster. However, if we double the mass of the Earth, it does not affect the speed with which it orbits the Sun. Why not? Because the Earth is soooo much smaller than the Sun that increasing a planet’s size generally doesn’t make a difference in the orbital speed. If you’re working with two objects about the same size, of course, then changing one of the masses absolutely has an effect on the other.
Click here to go to next lesson on Fun Activity with Kepler’s Laws.
[/am4show]
Kepler’s Laws of planetary orbits explain why the planets move at the speeds they do. You’ll be making a scale model of the solar system and tracking orbital speeds.
Kepler’s 1st Law states that planetary orbits about the Sun are not circles, but rather ellipses. The Sun lies at one of the foci of the ellipse. Kepler’s 2nd Law states that a line connecting the Sun and an orbiting planet will sweep out equal areas in for a given amount of time. Translation: the further away a planet is from the Sun, the slower it goes.
[am4show have=’p8;p9;p17;p44;p90;’ guest_error=’Guest error message’ user_error=’User error message’ ]
Download Student Worksheet & Exercises
What are the planets in our solar system starting closest to the Sun? On a sheet of paper, write down a planet and label it with the name. Do this for each of the eight planets.
- Mercury is 0.39 AU (in a rocket it would take 2.7 months to go straight to Mercury from the Sun)
- Venus is 0.72 AU
- Earth is 1 AU (in a rocket it would take 7 months to go straight to Earth from the Sun)
- Mars is 1.5 AU
- Jupiter is 5.2 AU
- Saturn is 9.6 AU
- Uranus is 19.2 AU
- Neptune is 30.1 AU (in a rocket it would take 18 years to go straight to Neptune from the Sun)
Of course, we don’t travel to planets in straight lines – we use curved paths to make use of the gravitational pull of nearby objects to slingshot us forward and save on fuel.
- Now draw the location of the asteroid belt.
- Draw the position of the Kuiper Belt” and ask a student to draw and label it (beyond Neptune).
- Where are the five dwarf planets? They are in the Kuiper belt and the asteroid belt:
- Ceres (in the Asteroid belt, closer to Jupiter than Mars)
- Pluto (is 39.44 AU from the Sun)
- Haumea (43.3 AU)
- Makemake (45.8 AU)
- Eris. (67.7 AU)
Now for the fun part! You’ll need a group of friends to work together for this lab, so you have at least one student for each planet, one for the Sun, and two for the asteroid belts, and five for the dwarf planets. You can assign additional students to be moons of Earth (Moon), Mars (Phobos and Deimos), Jupiter (assign only 4 for the largest ones: Ganymede, Callisto, Io, and Europa), Saturn (again, assign only 4: Titan, Rhea, Iapetus, and Dione), Uranus (Oberon, Titania), and Neptune (Triton). If you still have extra students, assign one to Charon (Pluto’s binary companion) and one each to Hydra and Nix, which orbit Pluto and Charon. While you ask the students to walk around in a later step, the moons can circle while they orbit.
- First, walk outside to a very large area.
- Hand the Sun student the measuring tape.
- Ask Kuiper Belt student(s) to take the end of the measuring tape and begin walking slowly away from the Sun.
- With each student assigned to the distance shown, grab the measuring tape and walk along with it. Please be careful – measuring tapes can have sharp edges! You can use gloves when you grab the tape if you’ve got a sharp steel measuring tape to protect your hands. Ask the Sun to call out the distances periodically so the students know when it’s time to come up.
- What do you notice about the distances between the planets? The nearest star is 114.5 miles away!
- Ask the students to let go of the measuring tape, except for Neptune and the Sun. Everyone else gathers around you (a safe distance away, as Neptune is going to orbit the Sun).
- Using a stopwatch, notice how much time it takes Neptune to walk around the Sun while holding the measuring tape taut. How long did it take for one revolution?
- Now ask Mercury to take their position on the tape at the appropriate distance. Time their revolution as they walk around the Sun. How long did it take?
- How does this relate to the data you just recorded for Neptune and Mercury? You should notice that the speeds the kids were walking at were probably nearly the same, but the time was much shorter for Mercury. If you could swing them around (instead of having them walk), can you imagine how this would make Mercury orbit at a faster speed than Neptune?
- If you have it, you can illustrate how Kepler’s 2nd law works and relate it back to this experiment. Tie a ball to the end of a string and whirling it around in a circle. After a few revolutions, let the string wind itself up around your finger. As the string length shortens, the ball speeds up. As the planet moves inward, the planet’s orbital speed increases. The planet’s speed decreases the further from the Sun it is located.
- Ask one of the bigger students to take their position with the measuring tape, reminding them to keep the tape taut no matter what happens. When they start to walk around the Sun, have the Sun move with them a bit (a couple of feet is good). Let the students know that the planet also yanks on the Sun just as hard as the Sun yanks on the planet. Since the planet is much smaller than the Sun, you won’t see as much motion with the Sun.
- Optional demonstration to illustrate this idea: take a heavy bag (I like to use oranges) and spin it around as you whirl around in a circle. Do you notice the student leans back a bit to balance themselves as they swing around and around? This is the same principle, just on a smaller scale. The two objects (the bag and the student) are orbiting around a common point, called the center of mass. In our real solar system, the Sun has 99.85% of the mass, so the center of mass lies inside the Sun (although not at the exact center).
- Look at the length of your measuring tape. Find the data table you need to use in the tables. Circle the one you’re going to use or cross out the ones you’re not.
- Using a stopwatch, time Venus as they walk around the Sun while holding the measuring tape taut. How long did it take for one revolution? (Make sure the Sun doesn’t move much during this process like they did for the demonstration. We’re assuming the Sun is at the center.)
- Continue this for all the planets.
What’s Going On?
Johannes Kepler, a German mathematician and astronomer in the 1600s, was one of the key players of his time in astronomy. Among his best discoveries was the development of three laws of planetary orbits. He worked for Tycho Brahe, who had logged huge volumes of astronomical data, which was later passed onto to Kepler. Kepler took this information to design and develop his ideas about the movements of the planets around the Sun.
Kepler’s 1st Law states that planetary orbits about the Sun are not circles, but rather ellipses. The Sun lies at one of the foci of the ellipse. Well, almost. Newton’s Laws of Motion state that the Sun can’t be stationary, because the Sun is pulling on the planet just as hard as the planet is pulling on the Sun. They are yanking on each other. The planet will move more due to this pulling because it is less massive. The real trick to understanding this law is that both objects orbit around a common point that is the center of mass for both objects. If you’ve ever swung a heavy bag of oranges around in a circle, you know that you have to lean back a bit to balance yourself as you swing around and around. It’s the same principle, just on a smaller scale.
In our solar system the Sun has 99.85% of the mass, so the center of mass between the Sun and any other object actually lies inside the Sun (although not at the center).
Kepler’s 2nd Law states that a line connecting the Sun and an orbiting planet will sweep out equal areas in for a given amount of time. The planet’s speed decreases the further from the Sun it is located (actually, the speed varies inversely with the square‐root of the distance, but you needn’t worry about that). You can demonstrate this to the students by tying a ball to the end of a string and whirl it around in a circle. After a few revolutions, let the string wind itself up around your finger. As the string length shortens, the ball speeds up. As the planet moves inward, the planet’s orbital speed increases.
Embedded in the second law are two very important laws: conservation of angular moment and conservation of energy. Although those laws might sound scary, they are not difficult to understand. Angular momentum is distance multiplied by mass multiplied by speed. The angular momentum for one case must be the same for the second case (otherwise it wouldn’t be conserved). As the planet moves in closer to the Sun, the distance decreases. The speed it orbits the Sun must increase because the mass doesn’t change. Just like you saw when you wound the ball around your finger.
Energy is the sum of both the kinetic (moving) energy and the potential energy (this is the “could” energy, as in a
ball dropped from a tower has more potential energy than a ball on the ground, because it “could” move if released). For conservation of energy, as the planet’s distance from the Sun increases, so does the gravitational potential energy. Again, since the energy for the first case must equal the energy from the second case (that’s what conservation means), the kinetic energy must decrease in order to keep the total energy sum a constant value.
Kepler’s 3rd Law is an equation that relates the revolution period with the average orbit speed. The important thing to note here is that mass was not originally in this equation. Newton came along shortly after and did add in the total mass of the system, which fixed the small error with the equation. This makes sense, as you might imagine a Sun twice the size would cause the Earth to orbit faster. However, if we double the mass of the Earth, it does not affect the speed with which it orbits the Sun. Why not? Because the Earth is soooo much smaller than the Sun that increasing a planet’s size generally doesn’t make a difference in the orbital speed. If you’re working with two objects about the same size, of course, then changing one of the masses absolutely has an effect on the other.
Exercises
- If the Sun is not stationary in the center but rather gets tugged a couple of feet as the planet yanks on it, how do you think this will affect the planet’s orbit?
- If we double the mass of Mars, how do you think this will affects the orbital speed?
- If Mercury’s orbit is normally 88 Earth days, how long do you estimate Neptune’s orbit to be?
Click here to go to next lesson on Elliptical Orbits.
[/am4show]
If one of Kepler’s Laws describe the orbits of satellites as being an elliptical orbit, you might be wondering what an ellipse is! Here’s a really neat way to make an ellipse using a pencil and a rubber band:
Click here to go to next lesson on Applying Kepler’s Laws.
[/am4show]
Let’s try a few practice problems so you get more familiar with how to use and apply Kepler’s Laws to real world physics problems…
[am4show have=’p9;p58;’ guest_error=’Guest error message’ user_error=’User error message’ ]
Click here to go to next lesson on Jupiter’s Moons.
[/am4show]
A satellite is an object that orbits the sun, earth or other massive body like a planet, moon, asteroid, or even galaxy. There are two kinds of satellites: natural, like the moon, and man-made, like the Hubble Space Telescope.
[am4show have=’p9;p58;’ guest_error=’Guest error message’ user_error=’User error message’ ]
Click here to go to next lesson on New Planets.
[/am4show]
But physics doesn’t care if a satellite is man-made or not. The laws of physics and math equations still apply no matter where the satellite came from.
[am4show have=’p9;p58;’ guest_error=’Guest error message’ user_error=’User error message’ ]
Click here to go to next lesson on Why Satellites Stay in Orbit.
[/am4show]
An important concept to understand is that a satellite is a projectile, meaning that only the force of gravity is acted on it (once it’s launched). In order to maintain it’s orbit, a satellite needs to fall continuously at the same rate that the earth is curving away from it.
[am4show have=’p9;p58;’ guest_error=’Guest error message’ user_error=’User error message’ ]
Click here to go to next lesson on Satellite Crash!
[/am4show]
The Hubble Space Telescope (HST) zooms around the Earth once every 90 minutes (about 5 miles per second), and in August 2008, Hubble completed 100,000 orbits! Although the HST was not the first space telescope, is the one of the largest and most publicized scientific instrument around. Hubble is a collaboration project between NASA and the ESA (European Space Agency), and is one of NASA’s “Great Observatories” (others include Compton Gamma Ray Observatory, Chandra X-Ray Observatory, and Spitzer Space Telescope). Anyone can apply for time on the telescope (you do not need to be affiliated with any academic institution or company), but it’s a tight squeeze to get on the schedule.
Hubble’s orbit zooms high in the upper atmosphere to steer clear of the obscuring haze of molecules in the sea of air. Hubble’s orbit slowly decays over time and begins to spiral back into Earth until the astronauts bump it back up into a higher orbit.
But how does a satellite stay in orbit? Try this experiment now:
Materials:
- marble
- paper
- tape
[am4show have=’p8;p9;p17;p44;p109;p96;’ guest_error=’Guest error message’ user_error=’User error message’ ]
Download Student Worksheet & Exercises
Troubleshooting: Expect to find marbles flying everywhere with this experiment! This quick activity demonstrates the idea of centripetal (centrifugal) acceleration. What happens when you circle the cone too slow or too fast? The marble itself is the satellite (like HST), and the cone’s apex (tip) is the Earth. When the marble zooms around too slow, it falls back into the Earth. So what keeps it up in “orbit”?
The faster an object moves, the greater the acceleration against the force of gravity (toward the Earth in this case). Think back to the Physics lab – when a marble went too slow through the roller coaster loop, it crashed back to the floor. When it went too fast, it flew off the track. There was a certain speed that was needed for the marble to stay in the loop and on course. The same is true for satellites in outer space.
If you have trouble with this experiment, just replace the paper cone with a disposable cup with a lid and try again (with the lid in place), and see if you can keep the marble circling around the top rim.
Exercises
- What happens when your marble satellite moves too slowly?
- What happens when the marble satellite orbits too fast?
- What effect does changing the marble mass have on your satellite speed?
- How is this model like the real thing?
Click here to go to next lesson on Saturn’s Moons.
[/am4show]
Kepler’s Law of Periods relates the period T of any planet around the sun to the cube of the semi-major axis a of the orbit:
[am4show have=’p9;p58;’ guest_error=’Guest error message’ user_error=’User error message’ ]
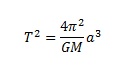
If T is in earth years, a is in AU (1 AU = distance from the sun to the earth), and M = solar mass, then the equation above reduces to: T2 = a3.
Click here to go to next lesson on Orbits of Satellites.
[/am4show]
A satellite is an object that does around a planet, a star, or other similar object. Here’s how you can figure out the net force of a satellite as well as the velocity of the satellite, since the only force applied to the satellite is from gravity:
[am4show have=’p9;p58;’ guest_error=’Guest error message’ user_error=’User error message’ ]
Click here to go to next lesson on Orbital Mechanics.
[/am4show]
For a satellite orbiting around the earth at a given distance. What is the speed and acceleration of the satellite? Do you think you need to know the masses of the satellite and the earth, or just one?
[am4show have=’p9;p58;’ guest_error=’Guest error message’ user_error=’User error message’ ]
Click here to go to next lesson on Equations for Circular Motion.
[/am4show]
Here’s an overview of all the equations we’ve been using so far for our study in uniform circular motion:
[am4show have=’p9;p58;’ guest_error=’Guest error message’ user_error=’User error message’ ]
Click here to go to next lesson on How Fast is the Moon?
[/am4show]
How fast does the moon travel around the earth? And how far away is the moon really? Here’s a way to figure out!
[am4show have=’p9;p58;’ guest_error=’Guest error message’ user_error=’User error message’ ]
Click here to go to next lesson on Callisto.
[/am4show]
Callisto is one of Jupiter’s moons. Would it be really cool to be able to approximate the size of Jupiter based on watching the motion of Callisto? For example, if you knew how long it took Callisto to orbit around Jupiter, and the furthest distance it traveled away from it (both of which you could measure from a backyard telescope)? Here’s how:
[am4show have=’p9;p58;’ guest_error=’Guest error message’ user_error=’User error message’ ]
Click here to go to next lesson on Space Station Speed.
[/am4show]
One of the questions I get asked a lot is how fast does the International Space Station travel around the Earth? Here’s how to figure this out (hint: it’s a lot like the one we did previously with Jupiter and Callisto!)
[am4show have=’p9;p58;’ guest_error=’Guest error message’ user_error=’User error message’ ]
Finding the Mass of the Earth Now let’s estimate the mass of the Earth. You already know what it is (because we’ve been using it a lot in our previous calculations), so let’s pretend we don’t know and figure out first-hand.
Click here to go to next lesson on Halley’s Comet.
[/am4show]
Comet Hally takes 76 years to orbit around the sun, and in 1986 it came as close as it possibly could to the sun (89,000,000 km). Can we figure out how far the comet gets from the sun based on this information? Sure! Here’s how:
[am4show have=’p9;p58;’ guest_error=’Guest error message’ user_error=’User error message’ ]
Click here to go to next lesson on Weightlessness.
[/am4show]
So, here’s a question. If you are “weightless” in space, do you still have mass? Yes, the amount of stuff you’re made of is the same on Earth as it is in your space ship. Mass does not change but since weight is a measure for how much gravity is pulling on you, weight will change. Did you notice that I put weightless in quotation marks? Wonder why?
[am4show have=’p9;p58;’ guest_error=’Guest error message’ user_error=’User error message’ ]
Weightlessness is a myth! Believe it or not, one is never weightless. A person can be pretty close to weightless in very deep space but the astronauts in a space ship actually do have a bit of weight.
Think about it for a second. If a space ship is orbiting the Earth what is it doing? It’s constantly falling! If it wasn’t moving forward at 10’s of thousands of miles an hour it would hit the Earth. It’s moving fast enough to fall around the curvature of the Earth as it falls but, indeed, it’s falling as the Earth’s gravity is pulling it to us.
Otherwise the ship would float out to space. So what is the astronaut doing? She’s falling too! The astronaut and the space ship are both falling to the Earth at the same rate of speed and so the astronaut feels weightless in space. If you were in an elevator and the cable snapped, you and the elevator would fall to the Earth at the same rate of speed. You’d feel weightless! (Don’t try this at home!)
Click here to go to next lesson on Physics Fun in an Elevator.
[/am4show]
Now let’s have fun with an elevator and a bathroom scale, since we can’t easily jump ourselves into orbit.
[am4show have=’p9;p58;’ guest_error=’Guest error message’ user_error=’User error message’ ]
Click here to go to next lesson on Bust a Myth.
[/am4show]
Now let’s bust the myth of weightlessness in space for good…
[am4show have=’p9;p58;’ guest_error=’Guest error message’ user_error=’User error message’ ]
Click here to go to next lesson on Binary System.
[/am4show]
A binary system exists when objects approach each other in size (and gravitational fields), the common point they rotate around (called the center of mass) lies outside both objects and they orbit around each other. Astronomers have found binary planets, binary stars, and even binary black holes.
The path of a planet around the Sun is due to the gravitational attraction between the Sun and the planet. This is true for the path of the Moon around the Earth, and Titan around Saturn, and the rest of the planets that have an orbiting moon.
Materials
- Soup cans or plastic containers with holes punched (like plastic yogurt containers, butter tubs, etc.)
- String
- Water
- Sand
- Rocks
- Pebbles
- Baking soda
- Vinegar
[am4show have=’p8;p9;p17;p44;p83;’ guest_error=’Guest error message’ user_error=’User error message’ ]
Download Student Worksheet & Exercises
- Thread one end of the string through one of the holes and tie a strong knot. Really strong.
- Tie the other end through the other hole and tie off.
- Go outside.
- Fill your can partway with water.
- Move away from everyone before you start to swing your container in a gentle circle. As you spin faster and faster, notice where the water is inside the container.
- Now empty out the water and replace it with rocks. Spin again and fill out the data table.
- To make carbon dioxide gas, you’ll need to work with another lab team. Cover the bottom of your container with baking soda. Add enough vinegar so that the bubbles reach the top without overflowing. Wait patiently for the bubbles to subside. You now have a container filled with carbon dioxide gas (and a little sodium acetate, the leftovers from the reaction). Carefully pour this into the empty container from the other lab team. They can spin again and record their results. When they are done, borrow their container and give them yours so they can fill it for you.
What’s Going On?
The path of a planet around the Sun is due to the gravitational attraction between the Sun and the planet. This is true for the path of the Moon around the Earth, and Titan around Saturn, and the rest of the planets that have an orbiting moon.
Charon and Pluto orbit around each other due to their gravitational attraction to each other. However, Charon is not the moon of Pluto, as originally thought. Pluto and Charon actually orbit around each other. Pluto and Charon also are tidally locked, just like the Earth-Moon system, meaning that one side of Pluto is always faces the same side of Charon.
Imagine you have a bucket half full of water. Can you tilt a bucket completely sideways without spilling a drop? Sure thing! You can swing it by the handle, and even though it’s upside down at one point, the water stays put. What’s keeping the water inside the bucket?
Before we answer this, imagine you are a passenger in a car, and the driver is late for an appointment. They take a turn a little too fast, and you forgot to fasten your seat belts. The car makes a sharp left turn. Which way would you move in the car if they took this turn too fast? Exactly – you’d go sliding to the right. So, who pushed you?
No one! Your body wanted to continue in a straight line, but the car is turning, so the right side car door keeps pushing you to turn you in a curve – into the left turn. The car door keeps moving in your way, turning you into a circle. The car door pushing on you is called centripetal force. Centripetal means “center-seeking.” It’s the force that points toward the center of the circle you’re moving on. When you swing the bucket around your head, the bottom of the bucket is making the water turn in a circle and not fly away. Your arm is pulling on the handle of the bucket, keeping it turning in a circle and not letting it fly away. That’s centripetal force.
Think of it this way: If I throw a ball in outer space, does it go in a straight line or does it wiggle all over the place? Straight line, right? Centripetal force is the force needed to keep an object following a curved path.
Remember how objects will travel in a straight line unless they bump into something or have another force acting on them, such as gravity, drag force, and so forth? Well, to keep the bucket of water swinging in a curved arc, the centripetal force can be felt in the tension experienced by the handle (or your arm, in our case). Swinging an object around on a string will cause the rope to undergo tension (centripetal force), and if your rope isn’t strong enough, it will snap and break, sending the mass flying off in a tangent (straight) line until gravity and drag force pull the object to a stop. This force is proportional to the square of the speed – the faster you swing the object, the higher the force.
Exercises
- How is spinning the container like Pluto and Charon?
- What would happen if we cut the string while you are spinning? Which way would the container go?
- What happens if we triple the size of your container and what’s inside of it?
Click here to go to next lesson on What’s Up in the Sky?
[/am4show]
Today you get to learn how to read an astronomical chart to find out when the Sun sets, when twilight ends, which planets are visible, when the next full moon occurs, and much more. This is an excellent way to impress your friends.
The patterns of stars and planets stay the same, although they appear to move across the sky nightly, and different stars and planets can be seen in different seasons.
Materials:
- Printout of Stargazer’s Almanac
- Pencil
- Tape and scissors (optional)
- Ruler
[am4show have=’p8;p9;p44;p105;p73;p90;’ guest_error=’Guest error message’ user_error=’User error message’ ]
Download Student Worksheet & Exercises
- If your chart comes on two pages, you’ll need to cut the borders off at the top and bottom and tape them together so they fit perfectly.
- Use your ruler as a straight edge to help locate items as you read the chart.
- Print out copies of the almanac by clicking the image of the Skygazer’s Almanac. You can print it full-size on two pages, or size it to fit onto a single page. Since there’s a ton of information on it, it’s best read over two pages. This is an expired calendar to practice with.
- First, note the “hourglass” shape of the chart. Do you see how it’s skinnier in the middle and wider near the ends? Since it’s an astronomical chart that shows what’s up in the sky at night, the nights are shorter during the summer months, so the number of hours the stars are visible is a lot less than during the winter. You’ll find the hours of the night printed across the top and bottom of the chart (find it now) and the months and days of the year printed on the right and left side.
- Can you find the summer solstice on June 20? Use your finger and start on the left side between June 17 and June 24. The 20th is between those two dates somewhere. Here’s how you tell exactly…
- Look at the entire chart – do you see the little dots that make up little squares all over the chart, like a grid? Each dot in the vertical direction represents one day. There are eight dots on the vertical side of the box.
- Let’s say you want to find out what time Neptune rises on June 17. Go back to June 17, which has its own little set of dots. Follow the dots with your finger until you hit the line that says Neptune Rises. Stop and trace it up vertically to the top scale to read just after 11 p.m.
- Look again at the dot boxes. Each horizontal dot is 5 minutes apart, and every six dots there is a vertical line representing the half-hour. The line crosses between the second and third dot, so if you lived in a place where you can clearly see the eastern horizon and looked out at 11:07, you’d see Neptune just rising. Since Uranus and Neptune are so far away, though, you’d need a telescope to see them. So let’s try something you can find with your naked eye.
- Look at Oct 21. What time does Saturn set? (5:30p.m.).
- What other two planets set right afterward? (Mercury at 6:03 p.m. and Mars sets at 7:12 p.m.).
- When does Jupiter rise? (7:32 p.m.).
- What is Neptune doing that night of Oct. 21? (Neptune transits, or is directly overhead, at 8:07 p.m. and sets at 1:30 a.m.)
- What other interesting things happen on Oct. 21? (Betelgeuse, one of the bright stars in the constellation Orion, rises at 9:23 p.m. Sirius, the dog star, rises at 11:06 p.m. The Pleiades, also known as the Seven Sisters, are overhead at 1:42 a.m.)
- Let’s find out when the Moon rises on Oct. 21. You’ll find a half circle representing the Moon centered on 11:05 p.m. Which phase is the Moon at? First or third quarter? (First. You can tell if you look at the next couple of days to see if the Moon waxes or wanes. Large circles indicate one of the four main phases of the Moon.)
- When does the Sun rise and set for Oct. 21? First, find the nearest vertical set of dots and read the time (5:30 p.m.). Now subtract out the 5-minute dots until you get to the edge. You should read three dots plus a little extra, which we estimate to be 17 minutes. Sunset is at 5:13 p.m. on Oct 21.
- Note the fuzzy, lighter areas on both sides of the hourglass. That represents the twilight time when it’s not quite dark, but it’s not daylight either. There’s a thin dashed line that runs up and down the vertical, following the curve of the hourglass offset by about an hour and 35 minutes. That’s the official time that twilight ends and the night begins.
- Can you find a meteor shower? Look for a starburst symbol and find the date right in the center. Those are the peak times to view the shower, and it’s usually in the wee morning hours. The very best meteor showers are when there’s also a new Moon nearby.
- Notice how Mercury and Venus stay close by the edges of the twilight. You’ll find a half-circle symbol representing the day that they are furthest from the Sun as viewed from the Earth, which is the best date to view it. For Venus, the * indicates the day that it’s the brightest.
- What do you think the open circle means at sunset on May 20? (New Moon)
- Students that spot the “Sun slow” or “Sun fast” marks on the chart always ask about it. It’s actually rather complicated to explain, but here’s the best way to think about it. Imagine that the vertical timeline running down the center means noon, not midnight. Do you see a second line weaving back and forth across the noon line throughout the year? That’s the line that shows the when the Sun crosses the meridian. On Feb 5, the Sun crosses that meridian at 12:14, so it’s “running slow,” because it “should have” crossed the meridian at noon. This small variation is due to the axis tilt of the Earth. Note that it never gets much more than 15 minutes fast or slow. The wavy line that represents this effect is called the Equation of Time. We’ll be using that later when we make our own sundials and have to correct for the Sun not being where it’s supposed to be.
- Look at Mars and Saturn both setting around the same time on Aug. 14. When two event lines cross, you’ll find nearby an open circle with a line coming from the top right side, accompanied by a set of arrows pointing toward each other. This means conjunction, and is a time when you can see two objects at once. Usually the symbol isn’t right at the intersection, because one of the objects is rising or setting and isn’t clearly visible. On Aug. 14, you’ll want to view them a little before they set, so the symbol is moved to a time where you can see them both more clearly.
- Important to note: If your area uses daylight savings time, you’ll need to add one hour to the times shown on the chart.
- Time corrections for advanced students: This chart was made for folks living on the 40o north latitude and 90o west longitude lines (which is Peoria, Ill.).
- If you live near the standardized longitudes for Eastern Time (75o), Central (90o), Mountain (105o) or Pacific (120o), then you don’t have to correct the chart times you read. However, if you live a little west or east of these standardized locations, you need a correction, which looks like this:
- For every degree west, add four minutes to the time you read off the chart.
- For every degree east, subtract four minutes from the time.
- For example, if you lived in Washington, D.C. (which is 77o longitude), note that this is 2o west of the Eastern Time, so you’d add 8 minutes to the time you read off the chart. Memorize your particular adjustment and always use it.
- If your latitude isn’t 40o north, then you need to adjust the rise and set times like this:
- If you live north of 40o, then the object you are viewing will be in the sky for longer than the chart shows, as it will rise earlier and set later.
- If you live south of 40o, then the object you are viewing will be in the sky for less time than the chart shows, as it will rise later and set earlier.
- The easiest way to calculate this is to note what time an object should rise, and then watch to see when it actually appears against a level horizon. This is your correction for your location.
What’s Going On?
This is one of the finest charts I’ve ever used as an astronomer, as it has so much information all in one place. You’ll find the rise and set times for all eight planets, peak times for annual meteor showers, moon phases, sunrise and set times, and it gives an overall picture of what the evening looks like over the entire year. Kids can clearly see the planetary movement patterns and quickly find what they need each night. I keep one of these posted right by the door for everyone to view all year long.
- If you live near the standardized longitudes for Eastern Time (75o), Central (90o), Mountain (105o) or Pacific (120o), then you don’t have to correct the chart times you read. However, if you live a little west or east of these standardized locations, you need a correction, which looks like this:
Exercises
- Is Mercury visible during the entire year?
- In general, when and where should you look for Venus?
- When is the best time to view a meteor shower?
- Which date has the most planets visible in the sky?
Click here to go to next lesson on Build a Solar System.
[/am4show]
What would happen if our solar system had three suns? Or the Earth had two moons? You can find out all these and more with this lesson on orbital mechanics. Instead of waiting until you hit college, we thought we'd throw some university-level physics at you... without the hard math.
[am4show have='p8;p9;p17;p44;' guest_error='Guest error message' user_error='User error message' ]
To get you experienced with the force of gravity without getting lost in the math, there's an excellent computer program that allows you to see how multi-object systems interact. Most textbooks are limited to the interaction between a very large object, like the Earth, and much smaller objects that are very close to it, like the Moon. This seriously cuts out most of the interesting solar systems that are out there in the real universe.
The University of Colorado at Boulder designed a great system to do the hard math for you. Don't be fooled by the simplistic appearance - the physics behind the simulation is rock-solid... meaning that the results you get are exactly what scientists would predict to happen.
How do I design a solar system?
Go to the My Solar System simulation on the PhET website and carefully follow the instructions for each activity. Answer the questions and record your results before going on to the next activity. Click here to RUN the simulation. If that link doesn't work try this alternative.
Here's what you should see and do:
Download Student Worksheet & Exercises
Exercises:
- What effect does changing the mass of orbiting planet have on the diameter of the orbit?
- What effect does changing the speed have on a planet’s orbit?
- What happens to the planet's orbit when you increase the initial distance between the planet and the Sun?
- Find the mass values needed for a stable orbit. Circle the values on the table that make a stable orbit.
- Why don’t a feather and a brick hit the ground at the same time?
Click here to go to next lesson on Retrograde Motion.
[/am4show]
If you watch the moon, you’d notice that it rises in the east and sets in the west. This direction is called ‘prograde motion’. The stars, sun, and moon all follow the same prograde motion, meaning that they all move across the sky in the same direction.
However, at certain times of the orbit, certain planets move in ‘retrograde motion’, the opposite way. Mars, Venus, and Mercury all have retrograde motion that have been recorded for as long as we’ve had something to write with. While most of the time, they spend their time in the ‘prograde’ direction, you’ll find that sometimes they stop, go backwards, stop, then go forward again, all over the course of several days to weeks.
Here are videos I created that show you what this would look like if you tracked their position in the sky each night for an year or two.
[am4show have=’p8;p9;p17;p44;p105;p90;’ guest_error=’Guest error message’ user_error=’User error message’ ]
Mercury and Venus Retrograde Motion
This is a video that shows the retrograde motion of Venus and Mercury over the course of several years. Venus is the dot that stays centered throughout the video (Mercury is the one that swings around rapidly), and the bright dot is the sun. Note how sometimes the trace lines zigzag, and other times they loop. Mercury and Venus never get far from the sun from Earth’s point of view, which is why you’ll only see Mercury in the early dawn or early evening.
Retrograde Motion of Mars
You’ve probably heard of epicycles people used to use to help explain the retrograde motion of Mars. Have you ever wondered what the fuss was all about? Here’s a video that traces out the path Mars takes over the course of several years. Do you see our Moon zipping by? The planets, Sun, and Moon all travel along line called the ‘ecliptic’, as they all are in about the same plane.
Download Student Worksheet & Exercises
Exercises
- During which of the months does Mars appear to move in retrograde?
- Why does Mars appear to move backward?
- Which planets have retrograde motion?
[/am4show]
Click here to go to next lesson on Potential Energy in the Stars.
In our physics problems so far, we’ve kept the objects close to the earth so that the acceleration due to gravity g remains constant, and we defined the potential energy of an object on the surface of the earth to be zero. What if we look up and see three stars in a system and want to find out the gravitational potential energy of the system?
[am4show have=’p9;p58;’ guest_error=’Guest error message’ user_error=’User error message’ ]
Globular clusters have a HUGE amount of gravitational potential energy.
This image above is known as Messier 13 (M13) or NGC 6205, also called the Hercules Globular Cluster, is a home to 300,000 stars in the constellation of Hercules. Can you start to see how there’s an enormous amount of gravitational potential energy in the universe?
Click here to go to next lesson on Escape Speed.
[/am4show]
Let’s determine the gravitational potential energy of the earth-moon system as well as the speed needed to escape the Earth’s gravitational pull:
[am4show have=’p9;p58;’ guest_error=’Guest error message’ user_error=’User error message’ ]
Click here to go to next lesson on Conservation of Mechanical Energy.
[/am4show]
Here’s how you put it all together and figure out the total energy of the system. This is useful when you’re trying to figure out something that you can’t otherwise solve for… let me show you with a set of videos here. Remember, for satellites the only force we have on the object is due to gravity, so the external work force term always goes to zero like this:
[am4show have=’p9;p58;’ guest_error=’Guest error message’ user_error=’User error message’ ]
Click here to go to next lesson on Geosynchronous Orbit.
[/am4show]
A geosynchronous orbit is an orbit that a satellite has when viewed from the earth, looks like the satellite is stationary.
[am4show have=’p9;p58;’ guest_error=’Guest error message’ user_error=’User error message’ ]
Click here to go to next lesson on Gravitational Potential Energy.
[/am4show]
How do you find the gravitational potential energy between two objects that are really far apart, like two stars or two galaxies? Here’s how:
[am4show have=’p9;p58;’ guest_error=’Guest error message’ user_error=’User error message’ ]
Click here to go to next lesson on Rocketship Races.
[/am4show]
Imagine you and I are racing rocketships in orbit around the Earth. I can slow down and still beat you around the Earth. Want to see how?
[am4show have=’p9;p58;’ guest_error=’Guest error message’ user_error=’User error message’ ]
Click here to go to next lesson on Equivalence Principle.
[/am4show]
Einstein once said: “I was sitting in a chair in the patent office at Bern when all of the sudden a thought occurred to me: If a person falls freely, he will not feel his own weight. I was startled. This simple thought made a deep impression on me. It impelled me toward a theory of gravitation.”
This led Einstein to develop his general theory of relativity, which interprets gravity not as a force but as the curvature of space and time. This topic is out of the scope for our lesson here, but you can explore more about it in this lesson.
The fundamental principle for relativity is the principle of equivalence, which says that if you were locked up in a box, you wouldn’t tell the difference between being in a gravitational field and accelerating (with an acceleration value equal to g) in a rocket.
The same thing is also true if you were either locked in a box, floating in outer space or in an elevator shaft experiencing free-fall. Any experiments you could do in either of those cases wouldn’t be able to tell you what was really happening outside your box. The way a ball drops is exactly the same in either case, and you would not be able to tell if you were falling in an elevator shaft or drifting in space.
[am4show have=’p9;p58;’ guest_error=’Guest error message’ user_error=’User error message’ ]
Have you ever seen an icicle? They usually grown downward toward the center of the earth (the direction of free-fall). But icicles on a car wheel grow radially outward because the wheel spins and flings the water toward the outside of the wheel where it freezes into spikes. The icicles can’t tell if the wheel is rotating and that’s why they grow radially, or it’s at rest at the gravitational field is in the radial direction!
Here’s a questions for you: these two astronauts (below) are inside the space station, which is currently in orbit around the earth. Which astronaut is upside down? Can you tell?
The principle of equivalence has some consequences! Navigation systems for ships, airplanes, missiles and submarines rely on acceleration information to calculate their velocity and position. However, the instruments that measure acceleration also react with unexpected variations in the earth’s gravitational field, and there’s no direct way to separate these two effect to avoid errors.
Highlights for Kepler’s Laws:
- The Law of Orbits: All planets move in elliptical orbits, with the sun at one focus.
- The Law of Areas: A line joining the planet to the sun sweeps out equal areas in equal times.
- The Law of Periods: The square of the period of any planet is proportional tot he cube of the semi-major axis of its orbit.
Yay! You completed this set of lessons on circular motion! Now it’s time for you to work your own physics problems!
Download your Circular Motion Problem Set here.
[/am4show]
Gravity is the reason behind books being dropped and suitcases feeling heavy. It’s also the reason our atmosphere sticks around and oceans staying put on the surface of the earth. Gravity is what pulls it all together, and we’re going to look deeper into what this one-way attractive force is all about.
[am4show have=’p9;p58;’ guest_error=’Guest error message’ user_error=’User error message’ ]
Galileo was actually one of the first people to do science experiment on gravity.Galileo soon figured out that objects could be the same shape and different weights (think of a golf ball and a ping pong ball), and they will still fall the same. It was only how they interacted with the air that caused the fall rate to change. By studying ramps (and not just dropping things), he could measure how long things took to drop using not a stopwatch but a water clock (imagine having a sink that regularly dripped once per second).
Whenever I teach a class about gravity, I’ll drop something (usually something large). After the heads whip around, I ask the hard question: “Why did it fall?”
You already know the answer – gravity. But why? Why does gravity pull things down, not up? And when did people first start noticing that we stick to the surface of the planet and not float up into the sky? No one can tell you why gravity is – that’s just the way the universe is wired. Gravitation is a natural thing that happens when you have mass.
Would it sound strange to you if I said that gravity propagates at the speed of light? If we suddenly made the sun disappear, the Earth’s orbit wouldn’t be instantaneously affected… it would take time for that information to travel to the earth. What does that mean? By the end of this section, you’ll be able to tell me about it. Let’s get started!
So far, saying the force of gravity is pretty comfortable. When you throw a ball high in the air, the force of gravity slows it down and as it falls back to the earth the force of gravity speeds the ball up. The force of gravity causes an acceleration during this flight, and is called the acceleration of gravity. The acceleration of gravity g is the acceleration experienced by an object when the only force acting on it is the force of gravity. This value of g is the same no matter how massive the object is. It’s always 9.81 m/s2.
Johannes Kepler, a German mathematician and astronomer in the 1600s, was one of the key players of his time in astronomy. Among his best discoveries was the development of three laws of planetary orbits. He worked for Tycho Brahe, who had logged huge volumes of astronomical data, which was later passed onto to Kepler. Kepler took this information to design and develop his ideas about the movements of the planets around the Sun. We’re going to go into deeper discussion about Kepler’s Laws in the next section, but here they are in a nutshell:
- The Law of Orbits: All planets move in elliptical orbits, with the sun at one focus.
- The Law of Areas: A line joining the planet to the sun sweeps out equal areas in equal times.
- The Law of Periods: The square of the period of any planet is proportional tot he cube of the semi-major axis of its orbit.
Did you notice that while Kepler’s Laws describe the motion of the planets around the sun, they don’t say why these paths are there? Kepler only hinted at an interaction between the sun and the planets to drive their motion, but not between the planets themselves, and it really was only a teensy hint.
Newton wasn’t satisfied with this explanation. He was determined to figure out the cause for the elliptical motion, especially since it wasn’t a circle or a straight line (remember Newton’s First Law: Objects in motion tend to stay in motion unless acted upon by an unbalanced force?) And circular motion needs centripetal force to keep the object following a curved path. So what force was keeping the planets in an ellipse around the sun?
Click here to go to next lesson on Inverse Square Law.
[/am4show]
One of Newton’s biggest contributions was figuring out how to show that gravity was the same force that caused both objects like an apple to fall to the earth at a rate of 9.81 m/s2 AND the moon being accelerated toward the earth but at a different rate of 0.00272 m/s2. If these are both due to the same force of gravity, why are they different numbers then? Why is the acceleration of the moon 1/3600th the acceleration of objects near the surface of the earth? It has to do with the fact that gravity decreases the further you are from an object. The moon is in orbit about 60 times further from the earth’s center than an object on the surface of the earth, which indicates that gravity is proportional to the inverse of the square of the distance (also called the inverse square law). So the force of gravity acts between any two objects and is inversely proportional to the square of the distance between the two centers. The further apart the objects are, the less they force of gravity is between the two of them. If you separate the objects by twice the distance, the gravitational force goes down by a factor of 4.
[am4show have=’p9;p58;’ guest_error=’Guest error message’ user_error=’User error message’ ]
Click here to go to next lesson on Applying the Inverse Square Law.
[/am4show]
All objects are attracted to each other with a gravitational force. You need objects the size of planets in order to detect this force, but everything, everywhere has a gravitational field and force associated with it. If you have mass, you have a gravitational attractive force. Newton’s Universal Law of Gravitation is amazing not because he figured out the relationship between mass, distance, and gravitational force (which is pretty incredible in its own right), but the fact that it’s universal, meaning that this applies to every object, everywhere.
[am4show have=’p9;p58;’ guest_error=’Guest error message’ user_error=’User error message’ ]
Newton suggested that every particle everywhere attracts every other particle with a force given by the following equation. If you have mass, then this force applies to you. Newton’s Universal Law of Gravitation is: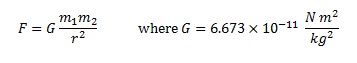 
That G is called the universal gravitation constant and is determined by doing experiments.
Click here to go to next lesson on Cavendish Experiment.
[/am4show]
Lord Henry Cavendish in 1798 (about a century after Newton) performed experiments with a torsion balance to figure out the value of G. It’s a very small number, so Cavendish had to carefully calibrate his experiment! The reason the number is so small is because we don’t see the effects of gravity until objects are very massive, like a moon or a planet in size.
[am4show have=’p9;p58;’ guest_error=’Guest error message’ user_error=’User error message’ ]
Cavendish used an experiment where two small lead spheres were fastened to the ends of a rod which had a very fine string (actually a quartz fiber) attached to the middle so it could be lifted off the ground. This is called a torsion balance, meaning that you can carefully measure the twist in the string by measuring how much the rod spins around. (Torsion balances can be made from other materials that have a stiffer spring constant value, like metal rods.) Back to his experiment: Cavendish placed two large lead spheres next to the smaller spheres, which moved the larger spheres and exerted a torque on the rod, and Cavendish was able to calculate the value of G.
The value of G is always the same, everywhere you go and any situation you apply it to. Once you know the masses and distances between objects, you can always calculate the force due to gravity with this one equation.
Although Newton’s Law of Gravitation applies only to particles, you can apply it to real objects as long as the sizes of the objects is small when you compare it to the distances between them.
You can concentrate an objects mass by shrinking it down to a particle using the idea of the center of mass like this:
Let’s practice it now…
Click here to go to next lesson on Star Wobble.
[/am4show]
How do astronomers find planets around distant stars? If you look at a star through binoculars or a telescope, you’ll quickly notice how bright the star is, and how difficult it is to see anything other than the star, especially a small planet that doesn’t generate any light of its own! Astronomers look for a shift, or wobble, of the star as it gets gravitationally “yanked” around by the orbiting planets. By measuring this wobble, astronomers can estimate the size and distance of larger orbiting objects.
Doppler spectroscopy is one way astronomers find planets around distant stars. If you recall the lesson where we created our own solar system in a computer simulation, you remember how the star could be influenced by a smaller planet enough to have a tiny orbit of its own. This tiny orbit is what astronomers are trying to detect with this method.
Materials
- Several bouncy balls of different sizes and weights, soft enough to stab with a toothpick
- Toothpicks
[am4show have=’p8;p9;p17;p44;p83;’ guest_error=’Guest error message’ user_error=’User error message’ ]
Download Student Worksheet & Exercises
- Does your ball have a number written on it? If so, that’s the weight, and you can skip measuring the weight with a scale.
- If not, weigh each one and make a note in the data table.
- Take the heaviest ball and spin it on the table. Can you get it to spin in place? That’s like a Sun without any planets around it.
- Insert a toothpick into the ball. Now insert the end of the toothpick into the smallest weight ball. Now spin the original ball. What happened?
What’s Going On?
Nearly half of the extrasolar (outside our solar system) planets discovered were found by using this method of detection. It’s very hard to detect planets from Earth because planets are so dim, and the light they do emit tends to be infrared radiation. Our Sun outshines all the planets in our solar system by one billion times.
This method uses the idea that an orbiting planet exerts a gravitational force on the Sun that yanks the Sun around in a tiny orbit. When this is viewed from a distance, the star appears to wobble. Not only that, this small orbit also affects the color of the light we receive from the star. This method requires that scientists make very precise measurements of its position in the sky.
Exercises
- For homework tonight, find out how many extrasolar planets scientists have detected so far.
- Also for homework, find out the names (they will probably be a string of numbers and letters together) of the 3 most recent extrasolar planet discoveries.
Click here to go to next lesson on If the Earth Gained Weight, Would You?
[/am4show]
Weight is nothing more than a measure of how much gravity is pulling on you. This is why you can be “weightless” in space. You are still made of stuff, but there’s no gravity to pull on you so you have no weight. The larger a body is, the more gravitational pull (or in other words the larger a gravitational field) it will have.
The Moon has a fairly small gravitational field (if you weighed 100 pounds on Earth, you’d only be 17 pounds on the Moon). The Earth’s field is fairly large and the Sun has a HUGE gravitational field (if you weighed 100 pounds on Earth, you’d weigh 2,500 pounds on the Sun!).
[am4show have=’p9;p58;’ guest_error=’Guest error message’ user_error=’User error message’ ]
As a matter of fact, the dog and I both have gravitational fields! Since we are both bodies of mass, we have a gravitational field which will pull things toward us. All bodies have a gravitational field. However, my mass is so small that the gravitational field I have is miniscule. Something has to be very massive before it has a gravitational field that noticeably attracts another body.
So what’s the measurement for how much stuff you’re made of? Mass. Mass is basically a weightless measure of how much matter makes you you. A hamster is made of a fairly small amount of stuff, so she has a small mass. I am made of more stuff, so my mass is greater than the hamster’s. Your house is made of even more stuff, so its mass is greater still.
So, here’s a question. If you are “weightless” in space, do you still have mass? Yes, the amount of stuff you’re made of is the same on Earth as it is in your space ship. Mass does not change, but since weight is a measure for how much gravity is pulling on you, weight will change.
Click here to go to next lesson on Turning the Sun into a Black Hole.
[/am4show]
At some point in the future you may ask yourself this question, “How can gravity pull harder (put more force on some things, like bowling balls) and yet accelerate all things equally?”
[am4show have=’p9;p58;’ guest_error=’Guest error message’ user_error=’User error message’ ]
Now that we have studied Newton’s laws, you can see that the above statement doesn’t make any sense at all! More force equals more acceleration is basically Newton’s Second law. The explanation for this is inertia.
Click here to go to next lesson on Gravity and Inertia.
[/am4show]
If you could stand on the Sun without being roasted, how much would you weigh? The gravitational pull is different for different objects. Let’s find out which celestial object you’d crack the pavement on, and which your lightweight toes would have to be careful about jumping on in case you leapt off the planet.
Weight is nothing more than a measure of how much gravity is pulling on you. Mass is a measure of how much stuff you’re made out of. Weight can change depending on the gravitational field you are standing in. Mass can only change if you lose an arm.
Materials
- Scale to weigh yourself
- Calculator
- Pencil
[am4show have=’p8;p9;p17;p44;p73;p83;’ guest_error=’Guest error message’ user_error=’User error message’ ]
Download Student Worksheet & Exercises
- We need to talk about the difference between weight and mass. In everyday language, weight and mass are used interchangeably, but scientists know better.
- Mass is how much stuff something is made out of. If you’re holding a bowling ball, you’ll notice that it’s hard to get started, and once it gets moving, it needs another push to get it to stop. If you leave the bowling ball on the floor, it stays put. Once you push it, it wants to stay moving. This “sluggishness” is called inertia. Mass is how much inertia an object has.
- Every object with mass also has a gravitational field, and is attracted to everything else that has mass. The amount of gravity something has depends on how far apart the objects are. When you step on a bathroom scale, you are reading your weight, or how much attraction is between you and the Earth.
- If you stepped on a scale in a spaceship that is parked from any planets, moons, black holes, or other objects, it would read zero. But is your mass zero? No way. You’re still made of the same stuff you were on Earth, so your mass is the same. But you’d have no weight.
- What is your weight on Earth? Let’s find out now.
- Step on the scale and read the number. Write it down.
- Now, what is your weight on the Moon? The correction factor is 0.17. So multiply your weight by 0.17 to find what the scale would read on the Moon.
- For example, if I weigh 100 pounds on Earth, then I’d weight only 17 pounds on the Moon. If the scale reads 10 kg on Earth, then it would read 1.7 kg on the Moon.
What’s Going On?
Weight is nothing more than a measure of how much gravity is pulling on you. This is why you can be “weightless” in space. You are still made of stuff, but there’s no gravity to pull on you so you have no weight. The larger a body is, the more gravitational pull (or in other words the larger a gravitational field) it will have.
The Moon has a fairly small gravitational field (if you weighed 100 pounds on Earth, you’d only be 17 pounds on the Moon).The Earth’s field is fairly large and the Sun has a HUGE gravitational field (if you weighed 100 pounds on Earth, you’d weigh 2,500 pounds on the Sun!).
As a matter of fact, the dog and I both have gravitational fields! Since we are both bodies of mass, we have a gravitational field which will pull things toward us. All bodies have a gravitational field. However, my mass is so small that the gravitational field I have is miniscule. Something has to be very massive before it has a gravitational field that noticeably attracts another body.
So what’s the measurement for how much stuff you’re made of? Mass. Mass is basically a weightless measure of how much matter makes you you. A hamster is made of a fairly small amount of stuff, so she has a small mass. I am made of more stuff, so my mass is greater than the hamster’s. Your house is made of even more stuff, so its mass is greater still. So, here’s a question. If you are “weightless” in space, do you still have mass? Yes, the amount of stuff you’re made of is the same on Earth as it is in your space ship. Mass does not change, but since weight is a measure for how much gravity is pulling on you, weight will change.
Did you notice that I put weightless in quotation marks? Wonder why?
Weightlessness is a myth! Believe it or not, one is never weightless. A person can be pretty close to weightless in very deep space, but the astronauts in a space ship actually do have a bit of weight.
Think about it for a second. If a space ship is orbiting the Earth, what is it doing? It’s constantly falling! If it wasn’t moving forward at tens of thousands of miles an hour it would hit the Earth. It’s moving fast enough to fall around the curvature of the Earth as it falls but, indeed, it’s falling as the Earth’s gravity is pulling it to us.
Otherwise the ship would float out to space. So what is the astronaut doing? She’s falling, too! The astronaut and the space ship are both falling to the Earth at the same rate of speed and so the astronaut feels weightless in space. If you were in an elevator and the cable snapped, you and the elevator would fall to the Earth at the same rate of speed. You’d feel weightless! (Don’t try this at home!)
Either now, or at some point in the future you may ask yourself this question, “How can gravity pull harder (put more force on some things, like bowling balls) and yet accelerate all things equally?” When we get into Newton’s laws in a few lessons, you’ll realize that doesn’t make any sense at all. More force equals more acceleration is basically Newton’s Second law.
Well, I don’t want to take too much time here since this is a little deeper then we need to go but I do feel some explanation is in order to avoid future confusion. The explanation for this is inertia. When we get to Newton’s First law we will discuss inertia. Inertia is basically how much force is needed to get something to move or stop moving.
Now, let’s get back to gravity and acceleration. Let’s take a look at a bowling ball and a golf ball. Gravity puts more force on the bowling ball than on the golf ball. So the bowling ball should accelerate faster since there’s more force on it. However, the bowling ball is heavier so it is harder to get it moving. Vice versa, the golf ball has less force pulling on it but it’s easier to get moving. Do you see it? The force and inertia thing equal out so that all things accelerate due to gravity at the same rate of speed!
Gravity had to be one of the first scientific discoveries. Whoever the first guy was to drop a rock on his foot, probably realized that things fall down! However, even though we have known about gravity for many years, it still remains one of the most elusive mysteries of science. At this point, nobody knows what makes things move toward a body of mass.
Why did the rock drop toward the Earth and on that guy’s foot? We still don’t know. We know that it does, but we don’t know what causes a gravitational attraction between objects. Gravity is also a very weak force. Compared to magnetic forces and electrostatic forces, the gravitational force is extremely weak. How come? No one knows. A large amount of amazing brain power is being used to discover these mysteries of gravity. Maybe it will be you who figures this out!
Exercises
- Of the following objects, which ones are attracted to one another by gravity?
a) Apple and Banana b) Beagle and Chihuahua c) Earth and You d) All of the above - True or False: Gravity accelerates all things differently
- True or False: Gravity pulls on all things differently
- If I drop a golf ball and a golf cart at the same time from the same height, which hits the ground first?
- There is a monkey hanging on the branch of a tree. A wildlife biologist wants to shoot a tranquilizer dart at the monkey to mark and study him. The biologist very carefully aims directly at the shoulder of the monkey and fires. However, the gun makes a loud enough noise that the monkey gets scared, lets go of the branch and falls directly downward. Does the dart hit where the biologist was aiming, or does it go higher or lower then he aimed? (This, by the way, is an old thought problem.)
Click here to go to next lesson on Rockets and Gravity.
[/am4show]
What happens to gravity if you’re in a rocket moving up through the atmosphere to a satellite in orbit?
[am4show have=’p9;p58;’ guest_error=’Guest error message’ user_error=’User error message’ ]
Does it remain the same or does it change during your flight? Here’s information about the earth:
- Radius: 3,959 miles (6,371 km)
- Distance from Sun: 92,960,000 miles (149,600,000 km)
- Mass: 5.972E24 kg
The International Space Station, an object about 72 meters long by 108 meters wide and 20 meters high stays in an orbital altitude of between 330 km (205 miles) and 410 km (255 miles), and moves at a rate of 27,724 kph(17,227 mph).
Click here to go to next lesson on Gravity for Different Objects.
[/am4show]
First we’re going to assume the earth is like a ball in that it’s a perfect sphere, and also that the density of the earth is even and it depends only how far from the center of the earth you are. Let’s also assume the earth isn’t rotating. Once we have these things in mind, then the magnitude of the force of gravity acting on an object goes like this…
[am4show have=’p9;p58;’ guest_error=’Guest error message’ user_error=’User error message’ ]
Click here to go to next lesson on Earth’s Crust is not Uniform.
[/am4show]
These are the scientific concepts students learn, separated by grade level according to both the national standards for science and Aurora’s personal experience in working with kids for nearly two decades. The scientific concepts are organized into categories within each grade level. You’ll find some areas span more than one grade level, so you will see some experiments listed for multiple grade levels.
PRE-K & K
Material properties, introduction to forces and motion, plants and animals, and basic principles of earth science.
First Grade
States of matter, weather, sound energy, light waves, and experimenting with the scientific method.
Second Grade
Chemical reactions, polymers, rocks and minerals, genetic traits, plant and animal life cycles, and Earth's resources.
Third Grade
Newton's law of motion, celestial objects, telescopes, measure the climate of the Earth and discover the microscopic world of life.
Fourth Grade
Electricity and magnetism, circuits and robotics, rocks and minerals, and the many different forms of energy.
Fifth Grade
Chemical elements and molecules, animal and plant biological functions, heat transfer, weather, planetary and solar astronomy.
Sixth Grade
Heat transfer, convetion currents, ecosystems, meteorology, simple machines, and alternative energy.
Seventh Grade
Cells, genetics, DNA, kinetic and potential, thermal energy, light and lasers, and biological structures.
Eighth Grade
Acceleration, forces projectile motion chemical reactions, deep space astronomy, and the periodic table.
High School (Advanced)
Alternative energy, astrophysics, robotics, chemistry, electronics, physics and more. For high school & advanced 5-8th students.
Teaching Resources
Tips and tricks to getting the science education results you want most for your students.
Science Fair Projects
Hovercraft, Light Speed, Fruit Batteries, Crystal Radios, R.O.V Underwater Robots and more!
There are three main differences between assuming the earth is round, uniformly dense, and not rotating as we did before.
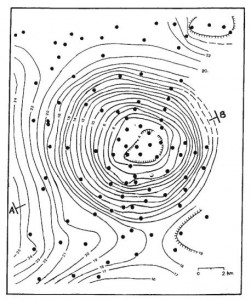First, the crust is not uniform. There are lumps and clumps everywhere that vary the density add up to make small variations in the force of gravity that we can actually measure with objects in free-fall motion. It’s actually how scientists find pockets of oil in the earth. They measure the surface gravity and plot it out, and if there’s a large enough deviation, it means there’s something interesting underground.
This image of the Mors salt dome in Denmark was studied for radioactive waste disposal. It’s a surface gravity survey that measures the acceleration due to gravity that shows something interesting is underground! The dots are the places where gravity was actually measured. You can read more about how gravity is measured from advanced lecture notes here. The unit of measurement for these deviations is called the “milligal” for Galileo, where 1 gal = 1,000 mgal = 1 cm/s3.
Click here to go to next lesson on The Earth is not a Sphere.
[/am4show]
The second problem with our assumption sis that the earth is not a sphere. It’s flattened a bit at the poles and bulges out at the equator. The ring around equator is larger than a ring around the poles by 21 km, which makes the poles closer to the center of the earth than the equator! Free-fall at the poles is slightly more than free-fall at the equator.
But before you book a trip to skydive in Ecuador, Colombia, Brazil, Sao Tome, Gabon, the Republic of the Congo, the Democratic Republic of the Congo, Uganda, Kenya, Somalia, Maldives, Indonesia or Kiribati, let’s talk about the assumption we made… The earth really does rotate. That’s not a surprise. How does this affect the value of g then? The bottom line is that gravity changes with altitude from 9.78 to 9.84 m/s2., mostly due to the earth spinning, but some to the earth not being a perfect sphere.
[am4show have=’p9;p58;’ guest_error=’Guest error message’ user_error=’User error message’ ]
Here are the Scientific Concepts to remember about Gravity:
- Gravity is a force that attracts things to one another.
- All bodies (objects) have a gravitational field.
- The larger a body is, the greater the strength of the gravitational field.
- Bodies must be very, very large before they exert any noticeable gravitational field.
- Gravity accelerates all things equally. Which means all things speed up the same amount as they fall.
- Gravity does not care what size things are or whether things are moving. All things are accelerated towards the Earth at the same rate of speed.
- Gravity does pull on things differently. Gravity is pulling greater on objects that weigh more.
- Weight is a measure of how much gravity is pulling on an object.
- Mass is a measure of how much matter (how many atoms) make up an object.
Click here to go to next lesson on Planetary and Satellite Motion.
[/am4show]
Circular motion is a little different from straight-line motion in a few different ways. Objects that move in circles are roller coasters in a loop, satellites in orbit, DVDs spinning in a player, kids on a merry go round, solar systems rotating in the galaxy, making a left turn in your car, water through a coiled hose, and so much more.
[am4show have=’p9;p58;’ guest_error=’Guest error message’ user_error=’User error message’ ]
Click here to go to next lesson on Introduction to Circular Motion.
[/am4show]
Imagine driving your car in a circle, like you would when take a clover-leaf type of freeway exit, or make a right turn on a green light. Here’s how the forces play out during the motion:
[am4show have=’p9;p58;’ guest_error=’Guest error message’ user_error=’User error message’ ]
Click here to go to next lesson on Calculating Average Speed.
[/am4show]
For any object that goes in a circle (or you can approximate it to a circle), you’ll want to use this approach when solving problems. You can feel the effect of circular motion if you’ve ever been in a car that suddenly turns right or left. You feel a push to the opposite side, right? If you are going fast enough and you take the turn hard enough, you can actually get slammed against the door. So my question to you is: who pushed you? Let’s find out!
[am4show have=’p9;p58;’ guest_error=’Guest error message’ user_error=’User error message’ ]
Click here to go to next lesson on Acceleration in a Circle.
[/am4show]
An object that moves in a circle with constant speed (like driving your car in a big circle at 30 mph) is called uniform circular motion. Although the speed is constant (30 mph), the velocity, which is a vector and made up of speed and direction, is not constant. The velocity vector has the same speed (magnitude), but the direction keeps changing as your car moves around the circle. The direction is an arrow that’s tangent to the circle as long as the car is moving on a circular path. This means that the tangent arrow is constantly changing and pointing in a new direction.
[am4show have=’p9;p58;’ guest_error=’Guest error message’ user_error=’User error message’ ]
It’s a common assumption that if the speed is constant, then there’s no acceleration… right?
Nope!
If the velocity is constant, then there’s no acceleration. But for circular motion, it’s speed, not velocity that is constant. Velocity is changing as the car turns a corner because the direction is changing, which also means that there is acceleration also! An accelerating object changes it’s velocity… it can be changing it’s speed, direction, or both. So objects moving in a circle are accelerating because they are always changing their direction.
Click here to go to next lesson on Accelerometer.
[/am4show]
A common misconception in science is that centrifugal and centripetal force (or acceleration) are the same thing. These two terms constantly throw students into frenzy, mostly because there is no clear definition in most textbooks. Here’s the scoop: centripetal and centrifugal force are NOT the same thing!
This experiment is mostly for Advanced Students, but here's a quick lesson you can do with your younger students...
[am4show have='p8;p9;p12;p39;p92;' guest_error='Guest error message' user_error='User error message' ] Before we jump in, let's recap what we've learned so far. A ball sitting still has a position you can chart on a map (latitude, longitude, and altitude), but no velocity or acceleration, because it's not moving. When you kick the ball, that's when it gets interesting. The second your toe touches the ball, things start to change. Velocity is a change of position. If you kick the ball ten feet, and it takes five seconds to go the distance, the average speed of the ball is 2 feet per second (about 1.4 MPH).
The trickier part of this scenario has to do with acceleration, which is the change in velocity. When you drive on the freeway at a constant 65 MPH, your acceleration is zero. Your speed does not change, so you have no acceleration. Your position is constantly changing, but you have constant speed. For example, when you enter the freeway, your speed changes from zero to 65 MPH in, say, ten seconds. Your acceleration is greatest when your foot first hits the gas – when your speed changes the most – when you’re moving from zero to a higher speed.
There's an interesting effect that happens when you travel in a curve. You can feel the effect of a different type of acceleration when you suddenly turn your car to the right – you will feel a push to the left. If you are going fast enough and you take the turn hard enough, you can get slammed against the door. So - who pushed you?
Think back to the first law of motion. An object in motion tends to stay in motion unless acted upon by an external force. This is the amazing part – the car is the external force. Your body was the object in motion, wanting to stay in motion in a straight line. The car turns, and your body still tries to maintain its straight path, but the car itself gets in the way. When you slam into the car door, the car is turning itself into your path, forcing you to change direction.
This effect is true when you travel in a car or in a roller coaster. It's the reason the water stays in the bucket when you swing it over your head. Physical motion is everywhere, challenging toddlers learning to walk as well as Olympic downhill skiers to go the distance. Here's a quick experiment you can do right now to wrap your head around this idea: Here's what you need to find for these experiments:
Now let's take a deeper look at centripetal, centrifugal, and how you can measure the g-force when taking a sharp turn in your car:
[/am4show][am4show have='p9;p39;' guest_error='Guest error message' user_error='User error message' ]
Centrifugal (translation = “center-fleeing”) force has two different definitions, which also causes confusion. The inertial centrifugal force is the most widely referred to, and is purely mathematical, having to do with calculating kinetic forces using reference frames, and is used with Newton’s laws of motion. It’s often referred to as the ‘fictitious force’.
Reactive centrifugal force happens when objects move in a curved path. This force is actually the same magnitude as centripetal force, but in the opposite direction, and you can think of it as the reaction force to the centripetal force. Think of how you stand on the Earth… your weight pushes down on the Earth, and a reaction force (called the “normal” force) pushes up in reaction to your weight, keeping you from falling to the center of the Earth. A centrifugal governor (spinning masses that regulate the speed of an engine) and a centrifugal clutch (spinning disk with two masses separated by a spring inside) are examples of this kind of force in action.
What about the fictitious (inertial) centrifugal force? Well, if you imagine being inside the car as it is banking with the windows blacked out, you suddenly feel a magical ‘push’ toward the door away from the center of the bend. This “push” is the fictitious force invoked because the car’s motion and acceleration is hidden from you (the observer) in the reference frame moving within the car. Okay, enough talk for now. Let's make two acceleration-measuring instruments (called 'accelerometers') so you can jump, run, swing, and zoom around to find out how many g's you can pull. You're going to make a cork-accelerometer and a g-force ring, both of which are used by my students when I teach mechanical engineering dynamics.
Download Student Worksheet & Exercises
To use the accelerometer: invert the bottle and try to make the cork move about. Remember – it is measuring acceleration, which is the change in speed. It will only move when your speed changes. You can do this experiment in a car while doing your other vehicle experiment: Why Bother With Seatbelts?. The trouble with this accelerometer is that there are no measurements you can take - it's purely visual. This next activity is more accurate at measuring the number of g-s you pull in a sharp turn (whether in a vehicle or in a roller coaster!)
Get about a foot of tubing – the bigger the diameter, the easier it will be to read. Also get a barbed union (plastic barbs work just fine). Fill your tube halfway with COLORED water (it’s impossible to read when it’s clear). Blue, green, red… your choice of food dye additive. Make an O-shape using your barb to water-seal the junction. Grab hold of one side and hold the circle vertical, with the barb-end pointing to the sky. The water should fill the bottom half, and air fills the top half. Make sure there are equal amounts of water and air in your tube. Make a mark on the tube where the water meets the air with a black marker. This is your 0-g reading (relative, of course). No acceleration. Not a whole lot of fun.
Now, for your 1-g mark – measure up 45 degrees from the first mark. (If the top of the circle is 90 degrees, and the 0-g mark is zero degrees, find the halfway point and label it).
The 2-g mark is 22.5 degrees up from the 1-g mark.
3-g mark is 11.25 degrees up from the last mark. And 4-g is 5.6 degrees up from the last mark. (See a pattern? You can prove this mathematically in college, and it’s kind of fun to figure out!)
Now, next time mom drives around town, hold the tube in your hand so that the water line starts at the zero mark. When she pulls a turn, see how far it sloshes up and tell her how many g’s she pulled. We also used to have contests to see who could pull the most g’s while spinning in a circle. Have fun!
This experiment is mostly for Advanced Students, but here's a quick lesson you can do with your younger students...
[am4show have='p8;p9;p12;p39;p92;' guest_error='Guest error message' user_error='User error message' ] Before we jump in, let's recap what we've learned so far. A ball sitting still has a position you can chart on a map (latitude, longitude, and altitude), but no velocity or acceleration, because it's not moving. When you kick the ball, that's when it gets interesting. The second your toe touches the ball, things start to change. Velocity is a change of position. If you kick the ball ten feet, and it takes five seconds to go the distance, the average speed of the ball is 2 feet per second (about 1.4 MPH).
The trickier part of this scenario has to do with acceleration, which is the change in velocity. When you drive on the freeway at a constant 65 MPH, your acceleration is zero. Your speed does not change, so you have no acceleration. Your position is constantly changing, but you have constant speed. For example, when you enter the freeway, your speed changes from zero to 65 MPH in, say, ten seconds. Your acceleration is greatest when your foot first hits the gas – when your speed changes the most – when you’re moving from zero to a higher speed.
There's an interesting effect that happens when you travel in a curve. You can feel the effect of a different type of acceleration when you suddenly turn your car to the right – you will feel a push to the left. If you are going fast enough and you take the turn hard enough, you can get slammed against the door. So - who pushed you?
Think back to the first law of motion. An object in motion tends to stay in motion unless acted upon by an external force. This is the amazing part – the car is the external force. Your body was the object in motion, wanting to stay in motion in a straight line. The car turns, and your body still tries to maintain its straight path, but the car itself gets in the way. When you slam into the car door, the car is turning itself into your path, forcing you to change direction.
This effect is true when you travel in a car or in a roller coaster. It's the reason the water stays in the bucket when you swing it over your head. Physical motion is everywhere, challenging toddlers learning to walk as well as Olympic downhill skiers to go the distance. Here's a quick experiment you can do right now to wrap your head around this idea: Here's what you need to find for these experiments:
- bucket
- water
- outdoor area
- you
- clear tubing (about 12-18" long)
- nylon or metal barbed union that fits inside the tubing
- empty soda bottle
- clean wine cork
- string
Bucket Splash
Fill a bucket half-full with water. Grasp the handle and swing it over your head in a circle in the vertical direction. Try spinning around while holding the handle out in front of your chest to swing it in the horizontal plane. Vary your spin speed to find the minimum!Now let's take a deeper look at centripetal, centrifugal, and how you can measure the g-force when taking a sharp turn in your car:
[/am4show][am4show have='p9;p39;' guest_error='Guest error message' user_error='User error message' ]
For Advanced Students:
Centripetal (translation = “center-seeking” ) is the force needed to keep an object following a curved path. Remember how objects will travel in a straight line unless they bump into something or have another force acting on it (gravity, drag force, etc.)? Well, to keep the bucket of water swinging in a curved arc, the centripetal force can be felt in the tension experienced by the handle (or your arm, in our case). Swinging an object around on a string will cause the rope to undergo tension (centripetal force), and if your rope isn’t strong enough, it will snap and break, sending the mass flying off in a tangent (straight) line until gravity and drag force pull the object to a stop. This force is proportional to the square of the speed - the faster you swing the object, the higher the force.Centrifugal (translation = “center-fleeing”) force has two different definitions, which also causes confusion. The inertial centrifugal force is the most widely referred to, and is purely mathematical, having to do with calculating kinetic forces using reference frames, and is used with Newton’s laws of motion. It’s often referred to as the ‘fictitious force’.
Reactive centrifugal force happens when objects move in a curved path. This force is actually the same magnitude as centripetal force, but in the opposite direction, and you can think of it as the reaction force to the centripetal force. Think of how you stand on the Earth… your weight pushes down on the Earth, and a reaction force (called the “normal” force) pushes up in reaction to your weight, keeping you from falling to the center of the Earth. A centrifugal governor (spinning masses that regulate the speed of an engine) and a centrifugal clutch (spinning disk with two masses separated by a spring inside) are examples of this kind of force in action.
Say WHAT?!?
Don't worry if these ideas make your brain turn into a pretzel. Most college students take three courses in this before it makes sense to them. Here's one more example: imagine driving a car along a banked turn. The road exerts a centripetal force on the car, keeping the car moving in a curved path (the “banked” turn). If you neglected to buckle your seat belt and the seats have a fresh coat of Armor-All (making them slippery), then as the car turns along the banked curve, you get “shoved” toward the door. But who pushed you? No one – your body wanted to continue in a straight line but the car keeps moving in your path, turning your body in a curve. The push of your weight on the door is the reactive centrifugal force, and the car pushing on you is the centripetal force.What about the fictitious (inertial) centrifugal force? Well, if you imagine being inside the car as it is banking with the windows blacked out, you suddenly feel a magical ‘push’ toward the door away from the center of the bend. This “push” is the fictitious force invoked because the car’s motion and acceleration is hidden from you (the observer) in the reference frame moving within the car. Okay, enough talk for now. Let's make two acceleration-measuring instruments (called 'accelerometers') so you can jump, run, swing, and zoom around to find out how many g's you can pull. You're going to make a cork-accelerometer and a g-force ring, both of which are used by my students when I teach mechanical engineering dynamics.
Cork Accelerometer
Fill an empty soda bottle to the top with water. Modify the soda bottle cap as follows: attach a string 8-10" long to a clean wine cork. Hot glue the free end of the string to the inside of the cap. Place the cork and string inside the bottle and screw on the top (try to eliminate the air bubbles). The cork should be free to bob around when you hold the bottle upside-down.G-Force Ring Accelerometer
One more university-level gadget for demonstrating the fascinating world of physical dynamics. This quick homemade device roughly measures acceleration in “g’s”. We used it to measure the g-force on roller coasters at Six Flags Magic Mountain, and it worked just as well as the expensive ones you buy in scientific catalogs!The 2-g mark is 22.5 degrees up from the 1-g mark.
3-g mark is 11.25 degrees up from the last mark. And 4-g is 5.6 degrees up from the last mark. (See a pattern? You can prove this mathematically in college, and it’s kind of fun to figure out!)
Now, next time mom drives around town, hold the tube in your hand so that the water line starts at the zero mark. When she pulls a turn, see how far it sloshes up and tell her how many g’s she pulled. We also used to have contests to see who could pull the most g’s while spinning in a circle. Have fun!
Advanced Students:
Advanced Students: Download your G-Force lab here. Exercises- Which accelerometer was better at giving a visual representation of accelerating?
- Which one do you prefer? Why?
- What activity did you do that created the most acceleration?
- What does that tell you about acceleration?
Click here to go to next lesson on Rotating Candles.
[/am4show]Now this next experiment is a little dangerous (we’re going to be spinning flames in a circle), so I found a video by MIT that has a row of five candles sitting on a rotating platform (like a “lazy susan”) so you can see how it works.
The candles are placed inside a dome (or a glass jar) so that when we spin them, they aren’t affected by the moving air but purely by acceleration. So for this video above, a row of candles are inside a clear dome on a rotating platform. When the platform rotates, air inside the dome gets swung to the outer part of the dome, creating higher density air at the outer rim, and lower density air in the middle. The candle flames point inwards towards the middle because the hot gas in the flames always points towards lower density air. Source: http://video.mit.edu
Now you’re beginning to understand how an object moving in a circle experiences acceleration, even if the speed is constant.
So what direction is the acceleration vector?
It’s pointed straight toward the center of that circle.
Velocity is always tangent to the circle in the direction of the motion, and acceleration is always directed radially inward. Because of these two things, the acceleration that arises from traveling in a circle is called centripetal acceleration (a word created by Sir Isaac Newton). There’s no direct relationship between the acceleration and velocity vectors for a moving particle.
Click here to go to next lesson on Centripetal Force.
Do you remember when I asked you “Who pushed you?” when you were riding in a car that took a sharp turn? Well, the answer has to do with centripetal force. Centripetal (translation = “center-seeking” ) is the force needed to keep an object following a curved path.
Remember how objects will travel in a straight line unless they bump into something or have another force acting on it like gravity, friction, or drag force? Imagine a car moving in a straight line at a constant speed. You’re inside the car, no seat belt, and the seat is slick enough for you to slide across easily. Now the car turns and drives again at constant speed but now on a circular path. When viewed from above the car, we see the car following a circle, and we see you wanting to keep moving in a straight line, but the car wall (door), moves into your path and exerts a force on you to keep you moving in a circle. The car door is pushing you into the circle.
According to Newton’s second law of motion, if you are experiencing an acceleration you must also be experiencing a net force (F=ma). The direction of the net force is in the same direction as the acceleration, so for the example with you inside the car, there’s an inward force acting on you (from the car door) keeping you moving in a circle.
If you have a bucket of water and you’re swinging it around your head, in order to keep a bucket of water swinging in a circle, the centripetal force can be felt in the tension experienced by the handle. Swinging an object around on a string will cause the rope to undergo tension (centripetal force), and if your rope isn’t strong enough, it will snap and break, sending the mass flying off in a tangential straight line until gravity and drag force pull the object to a stop.
This force is proportional to the square of the speed, meaning that the faster you swing the object, the higher the magnitude of the force will be.
Remember Newton’s First Law? The law of inertia? It states that objects in motion tend to stay in motion with the same speed and direction unless acted upon by an unbalanced/external force. Which means that objects naturally want to continue going their straight and merry way (like you did in a straight line when you were inside the car) until an unbalanced force causes it to turn speed up or stop. Can you see how an unbalanced force is required for objects to move in a circle? There has to be a force pushing on the object, keeping in on a circular path because otherwise, it’ll go off in a straight line!
[am4show have=’p9;p58;’ guest_error=’Guest error message’ user_error=’User error message’ ]
Click here to go to next lesson on Earth-Satellite System.
[/am4show]
Every object moving in a circle will experience a force pushing or pulling it toward the center of the circle. Whether it’s a car making a turn and the friction force from the road are acting on the wheels of the car, or a bucket is swung around your head and the tension of the rope keeps it moving in a circle, they all have to have a force keeping them moving in that circle, and that force is called centripetal force. Without it, objects could never change their direction. Because centripetal force is tangent to the velocity vector, the force can change the direction of an object without changing the magnitude.
[am4show have=’p9;p58;’ guest_error=’Guest error message’ user_error=’User error message’ ]
Click here to go to next lesson on Another Earth-Satellite System Example.
[/am4show]
Let's do another example of a satellite system:[am4show have='p9;p58;' guest_error='Guest error message' user_error='User error message' ]
There's a lot of confusion around the difference between centripetal and centrifugal force. The confusion usually starts with a thought like this: "When I go on a ride, I am getting thrown to the outside (if it's like a fast merry-go-round) or being squashed down in my seat (if it's like a roller coaster loop), but either way I am being pushed away from the center of the circle."
Can you imagine thinking that? Lots of people do! Now let's see if we can punch a few holes in that thought so you can really see how it's not true at all.
First of all, without the inward force pushing on you to keep you in a circle, you would be going off in a straight line and not around the loop of the roller coaster. The track is exerting a force on you, pushing you toward the center of the circle.
Now here's a question for you: just because you feel like you're being thrown, does that mean there has to be a force causing this? Is there any other way to explain that sensation? (Think Newton's Laws!)
Imagine again yourself in a car making a turn. If we had a video camera above the car, you'd see you wanting to continue in a straight line, but the car is now moving into your path and exerting a force on you, pushing you into a circle. That's when you hit the door.
The trick to really seeing this is to get out of yourself and into a different perspective! Einstein made a famous observation that described if you were in a rocket (without windows so you can't view the outside world), you would not be able to tell if the rocket was in space accelerating, or if it were standing still and you were experiencing the same amount of acceleration due to gravity on a planet. Because of F=ma, you can experience these two situations and still feel the same and not be able to tell which is which!
Okay, so are you ready to tackle centrifugal force?
There's a lot of confusion around the difference between centripetal and centrifugal force. The confusion usually starts with a thought like this: "When I go on a ride, I am getting thrown to the outside (if it's like a fast merry-go-round) or being squashed down in my seat (if it's like a roller coaster loop), but either way I am being pushed away from the center of the circle."
Can you imagine thinking that? Lots of people do! Now let's see if we can punch a few holes in that thought so you can really see how it's not true at all.
First of all, without the inward force pushing on you to keep you in a circle, you would be going off in a straight line and not around the loop of the roller coaster. The track is exerting a force on you, pushing you toward the center of the circle.
Now here's a question for you: just because you feel like you're being thrown, does that mean there has to be a force causing this? Is there any other way to explain that sensation? (Think Newton's Laws!)
Imagine again yourself in a car making a turn. If we had a video camera above the car, you'd see you wanting to continue in a straight line, but the car is now moving into your path and exerting a force on you, pushing you into a circle. That's when you hit the door.
The trick to really seeing this is to get out of yourself and into a different perspective! Einstein made a famous observation that described if you were in a rocket (without windows so you can't view the outside world), you would not be able to tell if the rocket was in space accelerating, or if it were standing still and you were experiencing the same amount of acceleration due to gravity on a planet. Because of F=ma, you can experience these two situations and still feel the same and not be able to tell which is which!
Okay, so are you ready to tackle centrifugal force?
Click here to go to next lesson on Centrifugal Force.
[/am4show]
Centrifugal (translation = “center-fleeing”) force has two different definitions, which causes even more confusion. The inertial centrifugal force is the most widely referred to, and is purely mathematical, having to do with calculating kinetic forces using reference frames, and is used with Newton’s laws of motion. It’s often referred to as the ‘fictitious force’.
[am4show have=’p9;p58;’ guest_error=’Guest error message’ user_error=’User error message’ ]
Reactive centrifugal force happens when objects move in a curved path. This force is actually the same magnitude as centripetal force, but in the opposite direction, and you can think of it as the reaction force to the centripetal force. Think of how you stand on the Earth. Your weight pushes down on the Earth, and a reaction force (the “normal” force) pushes up in reaction to your weight, keeping you from falling to the center of the Earth.
A centrifugal governor (spinning masses that regulate the speed of an engine) and a centrifugal clutch (spinning disk with two masses separated by a spring inside) are examples of this kind of force in action.
Here’s anther example: imagine driving a car along a banked turn. The road exerts a centripetal force on the car, keeping the car moving in a curved path (the “banked” turn). If you neglected to buckle your seat belt and the seats have a fresh coat of Armor-All (making them slippery), then as the car turns along the banked curve, you get “shoved” toward the door. But who pushed you? No one – your body wanted to continue in a straight line but the car keeps moving in your path, turning your body in a curve. The push of your weight on the door is the reactive centrifugal force, and the car pushing on you is the centripetal force.
What about the fictitious (inertial) centrifugal force? Well, if you imagine being inside the car as it is banking with the windows blacked out, you suddenly feel a magical ‘push’ toward the door away from the center of the bend. This “push” is the fictitious force invoked because the car’s motion and acceleration is hidden from you (the observer) in the reference frame moving within the car.
James Watt invented a “centrifugal governor”, which is a closed loop mechanical device you’ll find in lawn mowers, cruise controls, and airplane propellers to automatically control the speed of these things. The heavy brass balls spin around, and the faster they go, the more they rise up, which increases the rotational energy of this device, and since it’s connected to the throttle of something like a lawn mower engine, it can be carefully set to maintain the same speed or output power of the engine. It’s an automatic feedback system that is purely mechanical. Source: Mirko Junge, Science Museum London.
For circular motion, there are a couple of equations we will need to tackle physics problems that involve speed (v), acceleration (a), and force (F):
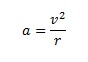
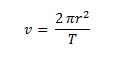
Here’s the equation for calculating centripetal force:
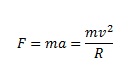
There’s another equation that relates the rotational speed (w) with the velocity like this:
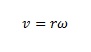
Here’s a cool experiment you can do that will really show you how objects that move in a circle experience centripetal force. You can lift at least 10 balls by using only one! All you need are balls, fishing line or dental floss, and an old pen.
Video note: Oops! I made a mistake. Around 5:00 it should be sqrt(10rg) not sqrt(20rg).
Let’s calculate the velocity of the above experiment using our new circular motion equations. Let’s say you timed yourself, and you can get one ball to lift five identical balls when the one ball swings around once every second. Let’s calculate the acceleration, force, and speed.
The net force acting on the ball is directed inwards. There might be more than one force acting on an object moving in a circle, but it’s the net force that adds them all up. The net force is proportional to the square of the speed (look at the equations again!). So if your speed increases three times, then the force increases by a factor of nine.
Click here to go to next lesson on Circular Motion with a Car.
[/am4show]
Let’s do a sample problem involving a car:
[am4show have=’p9;p58;’ guest_error=’Guest error message’ user_error=’User error message’ ]
Click here to go to next lesson on Circular Motion with a Kid.
[/am4show]
Now let’s do a similar problem but this time with a kid instead of a car:
[am4show have=’p9;p58;’ guest_error=’Guest error message’ user_error=’User error message’ ]
Click here to go to next lesson on Favorite Amusement Park Ride.
[/am4show]
I love amusement park rides, even though I know what’s going on from the science side of things! Here’s one that’s always been a favorite of mine:
[am4show have=’p9;p58;’ guest_error=’Guest error message’ user_error=’User error message’ ]
Click here to go to next lesson on Circular Motion and Friction.
[/am4show]
Before we go any further, we need to take a look at how friction gets handled in these types of problems:
[am4show have=’p9;p58;’ guest_error=’Guest error message’ user_error=’User error message’ ]
Click here to go to next lesson on Swinging Bucket.
[/am4show]
You’ve come so far with your analysis that I really want to give you the “real way” to solve these types of problems. Normally, this method isn’t introduced to you until your second year in college, and that’s only if you’re an engineer taking Statics and Dynamics classes (the next level after this course).
Here’s a step-by-step method that really puts all the pieces we’ve been working on all together into one:
[am4show have=’p9;p58;’ guest_error=’Guest error message’ user_error=’User error message’ ]
Do you see how easy that is? It puts the FBD (free body diagram) together with the MAD (mass-acceleration diagram) and uses Newton’s Laws to solve for the things you need to know. Using pictures and equations, you can solve anything now!
Click here to go to next lesson on Clothoid Loops.
[/am4show]
Let’s do something fun now… want to know about the physics of real roller coasters?
[am4show have=’p9;p58;’ guest_error=’Guest error message’ user_error=’User error message’ ]
It’s really important to know how much centrifugal force people experience, whether its in cars or roller coasters! In fact roller coaster loops used to be circular, but now they use clothoid loops instead to keep passengers happy during their ride so they don’t need nearly the acceleration that they’d need for a circular loop (which means less g-force so passengers don’t black out).
Click here to go to next lesson on Roller Coaster Maneuvers.
[/am4show]
There’s two main types of maneuvers a roller coaster can do that’s easy for us to analyze with uniform circular motion: camel-backs are the first one:
[am4show have=’p9;p58;’ guest_error=’Guest error message’ user_error=’User error message’ ]
…and loops are the second type of maneuver:
Click here to go to next lesson on Roller Coaster Activity.
[/am4show]
We’re going to build monster roller coasters in your house using just a couple of simple materials. You might have heard how energy cannot be created or destroyed, but it can be transferred or transformed (if you haven’t that’s okay – you’ll pick it up while doing this activity).
Roller coasters are a prime example of energy transfer: You start at the top of a big hill at low speeds (high gravitational potential energy), then race down a slope at break-neck speed (potential transforming into kinetic) until you bottom out and enter a loop (highest kinetic energy, lowest potential energy). At the top of the loop, your speed slows (increasing your potential energy), but then you speed up again and you zoom near the bottom exit of the loop (increasing your kinetic energy), and you’re off again!
Here’s what you need:
[am4show have=’p8;p9;p15;p42;p151;p75;p85;p88;p92;p100;’ guest_error=’Guest error message’ user_error=’User error message’ ]
- marbles
- masking tape
- 3/4″ pipe foam insulation (NOT neoprene and NOT the kind with built-in adhesive tape)
To make the roller coasters, you’ll need foam pipe insulation, which is sold by the six-foot increments at the hardware store. You’ll be slicing them in half lengthwise, so each piece makes twelve feet of track. It comes in all sizes, so bring your marbles when you select the size. The ¾” size fits most marbles, but if you’re using ball bearings or shooter marbles, try those out at the store. (At the very least you’ll get smiles and interest from the hardware store sales people.) Cut most of the track lengthwise (the hard way) with scissors. You’ll find it is already sliced on one side, so this makes your task easier. Leave a few pieces uncut to become “tunnels” for later roller coasters.
Read for some ‘vintage Aurora’ video? This is one of the very first videos ever made by Supercharged Science:
Download Student Worksheet & Exercises
Tips & Tricks
Loops Swing the track around in a complete circle and attach the outside of the track to chairs, table legs, and hard floors with tape to secure in place. Loops take a bit of speed to make it through, so have your partner hold it while you test it out before taping. Start with smaller loops and increase in size to match your entrance velocity into the loop. Loops can be used to slow a marble down if speed is a problem.
Camel-Backs Make a hill out of track in an upside-down U-shape. Good for show, especially if you get the hill height just right so the marble comes off the track slightly, then back on without missing a beat.
Whirly-Birds Take a loop and make it horizontal. Great around poles and posts, but just keep the bank angle steep enough and the marble speed fast enough so it doesn’t fly off track.
Corkscrew Start with a basic loop, then spread apart the entrance and exit points. The further apart they get, the more fun it becomes. Corkscrews usually require more speed than loops of the same size.
Jump Track A major show-off feature that requires very rigid entrance and exit points on the track. Use a lot of tape and incline the entrance (end of the track) slightly while declining the exit (beginning of new track piece).
Pretzel The cream of the crop in maneuvers. Make a very loose knot that resembles a pretzel. Bank angles and speed are the most critical, with rigid track positioning a close second. If you’re having trouble, make the pretzel smaller and try again. You can bank the track at any angle because the foam is so soft. Use lots of tape and a firm surface (bookcases, chairs, etc).
Troubleshooting Marbles will fly everywhere, so make sure you have a lot of extras! If your marble is not following your track, look very carefully for the point of departure – where it flies off.
-Does the track change position with the weight of the marble, making it fly off course? Make the track more rigid by taping it to a surface.
-Is the marble jumping over the track wall? Increase your bank angle (the amount of twist the track makes along its length).
-Does your marble just fall out of the loop? Increase your marble speed by starting at a higher position. When all else fails and your marble still won’t stay on the track, make it a tunnel section by taping another piece on top the main track. Spiral-wrap the tape along the length of both pieces to secure them together.
HOT TIPS for ULTRA-COOL PARENTS: This lab is an excellent opportunity for kids to practice their resilience, because we guarantee this experiment will not work the first several times they try it. While you can certainly help the kids out, it’s important that you help them figure it out on their own. You can do this by asking questions instead of rushing in to solve their problems. For instance, when the marble flies off the track, you can step back and say:
“Hmmm… did the marble go to fast or too slow?”
“Where did it fly off?”
“Wow – I’ll bet you didn’t expect that to happen. Now what are you going to try?”
Become their biggest fan by cheering them on, encouraging them to make mistakes, and try something new (even if they aren’t sure if it will work out).
Check out this cool roller coaster from one of our students!
Exercises
- What type of energy does a marble have while flying down the track of a roller coaster?
- What type of energy does the marble have when you are holding it at the top of the track?
- At the top of a camel back hill, which is higher for the marble, kinetic or potential energy?
- At the top of an inverted loop, which energy is higher, kinetic or potential energy?
Click here to go to next lesson on Speed Skating.
[/am4show]
You can find circular motion everywhere, including football, car racing, ice skating, and baseball. An ice skater spins on ice, or a competition speed skater makes a turn… they are both examples of circular motion. A turn happens when there’s a force component directed inward from the circular path. Let me show you a couple of examples:
[am4show have=’p9;p58;’ guest_error=’Guest error message’ user_error=’User error message’ ]
Click here to go to next lesson on Unbanked Car Turn without Friction.
[/am4show]
What about your car along a circular path? Let’s take a look at two different examples. The first is an unbanked turn with friction:
[am4show have=’p9;p58;’ guest_error=’Guest error message’ user_error=’User error message’ ]
Click here to go to next lesson on Banked Car Turn with Friction.
[/am4show]
The second example is a banked turn, like NASCAR racing:
[am4show have=’p9;p58;’ guest_error=’Guest error message’ user_error=’User error message’ ]
Click here to go to next lesson on Universal Gravitation.
[/am4show]