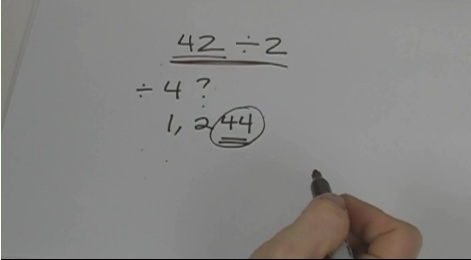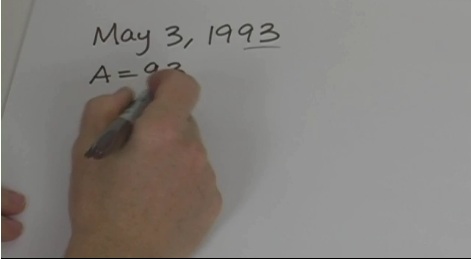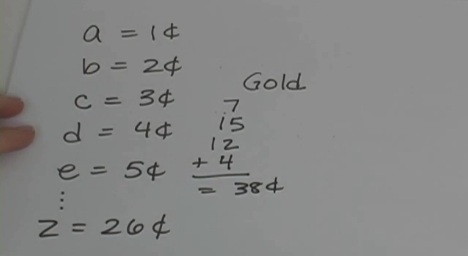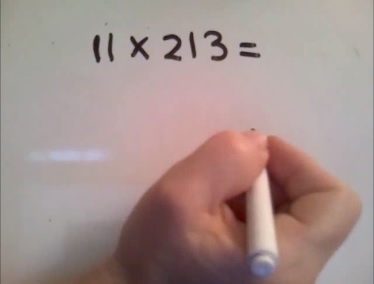If you haven’t memorized your multiplication table yet, I am going to show you how to you need to memorize only three of the 400 numbers on a 20 times table in order to know your table.

[am4show have='p8;p9;p11;p38;p92;' guest_error='Guest error message' user_error='User error message' ]

Having trouble with your 6, 7, 8, and 9 multiplication tables? Sneak a peek at this nifty trick for multiplying single digits together. All you need is a set of hands and about ten minutes, and you'll be a whiz and multiplying with your hands.
[am4show have='p8;p9;p11;p38;p92;' guest_error='Guest error message' user_error='User error message' ]

Download the student worksheet that goes with this lesson.
[/am4show]

One day, my kid asked me how a calculator comes up with its answers. That's a great question, I thought. How does a calculator do math?

After thinking about it, I realized this was a great way to teach him about binary numbers. I am going to show you how to not only count in binary, but also help you understand the basis of all electronic devices by knowing this key element.

[am4show have='p8;p9;p11;p38;p92;' guest_error='Guest error message' user_error='User error message' ]

Download the student worksheet that goes with this lesson.

By asking questions, you can discover a lot of what you already know about a subject. In this case, students usually know how to count to 100 or even 1,000, but they don’t consciously know why the numbers change in the sequence that they do. In this activity, we’re going to explore how quantities are represented by numerals (digits 0 through 9), and then learn how you can change the number of numerals and count in different bases. In the instructional video, we’re learning base 2 and 10, but you can use this to represent any base to count in.

Exercises

〖93〗^2
〖193〗^2
〖979〗^2
〖249〗^2
〖415〗^2
〖84〗^2
〖573〗^2
〖333〗^2
〖757〗^2
〖696〗^2
[/am4show]

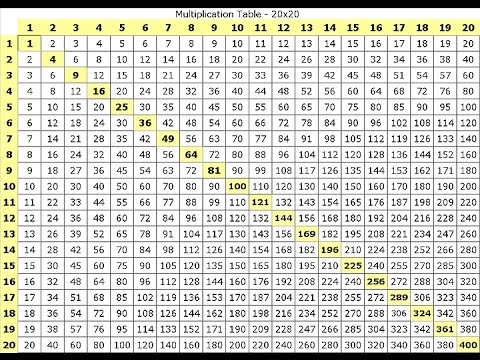
If you hate long division like I do, then this lesson will be very useful in showing you how to make the most out of your division tasks without losing sleep over it. It's easy, quick, and a whole lot of fun! If you haven’t already mastered your multiplication tables, make sure you have one handy to refer to as you go along.

[am4show have='p8;p9;p11;p38;p92;' guest_error='Guest error message' user_error='User error message' ]

Download the student worksheet that goes with this lesson.

Many, many thanks go to Arthur Benjamin, a mathematics professor extraordinaire and professional magician who inspired much of this content we covered today.
[/am4show]

If you don’t have the patience to do multiplication on paper for every single math problem that comes your way, then you’ll really enjoy this math lesson! You’ll be able to multiply one and two digit numbers in your head, which you’ll be able to use when checking your answers on a math test, or just whenever you need to multiply something quickly when paper’s not around.
[am4show have='p8;p9;p11;p38;p92;' guest_error='Guest error message' user_error='User error message' ]

Download the student worksheet that goes with this lesson.

If you haven’t already mastered your multiplication tables, make sure you have one handy to refer to as you go along.
[/am4show]

In school, you are trained to solve math problems on paper, at a desk. The problem with that is, for most people, math problems don’t usually come with a desk or a pencil. They pop up in the checkout line when paying for groceries, figuring out your gas mileage at the pump, or when counting calories at a restaurant. Learning how to solve math problems in your head is an essential everyday life skill, especially if you don’t want to be ripped off in money transactions.

[am4show have='p8;p9;p11;p38;p92;' guest_error='Guest error message' user_error='User error message' ]

Download the student worksheet that goes with this lesson.

Learning how to calculate in your head doesn’t have to be hard or scary, but it does require a little rewiring of the current math solving conditioning that you’ve already got in your brain. Specifically, we’re going to train your mind that when you solve math problems without paper, you must do it from left to right. It’s so much easier to think about math problems from left to right, so that’s how we’re going to do them.
[/am4show]

If you haven’t memorized your multiplication table yet, I am going to show you how to you need to memorize only three of the 400 numbers on a 20 times table in order to know your table.

[am4show have='p8;p9;p11;p38;p92;' guest_error='Guest error message' user_error='User error message' ]

Download the student worksheet that goes with this lesson.

Math isn’t about solving problems on any one particular way, but rather it’s about puzzling the solution out multiple ways! The times table is essential to doing math in your head, but you don’t need to know every cell on the table by heart. With a couple of quick tips and tricks, you’ll be able to know your table up to 20 without a lot of memorization simply by being clever about the way you go about it.
[/am4show]

This math lesson is so easy that one night, I wound up showing it to everyone in the pizza restaurant. Well, everyone who would listen, anyway. We were scribbling down the answers right on the pizza boxes with such excitement that I couldn’t help it – I started laughing right out loud about how excited everyone was about math - especially on a Saturday night.

[am4show have='p8;p9;p11;p38;p92;' guest_error='Guest error message' user_error='User error message' ]

Download the student worksheet that goes with this lesson.

When you do this calculation in front of friends or family, it’s more impressive if you hand a calculator out first and let them know that you are ‘testing to see if the calculator is working right’. Ask for a two digit number and have them check the calculator’s answer against yours.
[/am4show]

Do you think you'll need to know how to multiply by 12 or 11 more? Think of it this way: how often do you need to figure out how many dozen you need of something? It comes up a lot more than needing to know how many batches of 11, doesn't it? That's because of the way we've decided to group things mathematically as a society.

Here's why: We picked 12 based on how we used to count on our fingers using the "finger segment" system. If you look at your hands, you'll notice that your index finger has three segments to it. So does your middle finger, ring finger, and pinkie. Since you have four fingers, you actually have 12 sections for counting with (we're not including your thumb, which is the pointer... your thumb rests on the section you're currently on). When your thumb touches the tip of your index finger, that means "1". When your thumb touches the middle segment, that's "2", and the base segment is "3". The tip of your middle finger is "4", and so on. That's how we came to use the 12-in-a-batch system.

If you're wondering why we didn't use the 24-in-a-batch system (because you have two hands), that's because one hand was for 1-12 and the second hand indicated the number of batches of 12. So if your left hand has your thumb on the ring finger's base segment (9) and your right hand has the thumb touching the index finger's middle segment (2 complete batches of 12, or 2 x 12), the number you counted to is: 24 + 9 = 33.

Fortunately we now have calculators and a base-ten system, so this whole thing worked out well. But still the number 12 persists! So I thought you'd like this video, which expands on the idea of quickly multiplying two-digit numbers and three-digit numbers by eleven. This is very similar to the shortcut used when multiplying by eleven, but it also involves some doubling. Are you ready?

[am4show have='p8;p9;p11;p38;p92;p154;' guest_error='Guest error message' user_error='User error message' ]

Download Student Worksheet & Exercises

Isn’t this a really cool (and FAST) way to multiply by twelve? It's a lot faster than using the Babylonian finger-segment system. Try some problems on your own and check your work with a calculator.

How do you think this works?

1. 11 x 543
2. 12 x 45
3. 12 x 326
4. 12 x 769
5. 12 x 1345
6. 12 x 3461
7. 12 x 7532
8. 12 x 8989
9. 12 x 9999
10. 12 x 98749

[/am4show]

Can you look at a number and tell right away if it’s divisible by another number? Well, it’s pretty easy for 2 – if it’s an even number, it’s definitely divisible by two. Testing whether a number is divisible by five is easy as well. How can you tell?

In this video, I’ll show you some tricks to determine if a number is divisible by 3, 4, 6 and 7 before you start to divide. Some are simple and fast and some are a bit more complex. These can be very useful tricks for working with larger numbers (or just really fun to play with for a bit).

[am4show have='p8;p9;p11;p38;p92;p154;' guest_error='Guest error message' user_error='User error message' ]

Download Student Worksheet & Exercises

It’s pretty complex to be able to tell if a number is divisible by 7, but I think it's really neat that there’s a way to figure it out before you actually do the math. What do you think?

Exercises

1. Identify the number(s) that are divisible by 2 in the following list.
   301, 3645, 3673
2.  Identify the numbers that are divisible by 3 in the following list.
   3981, 430, 4598, 72624
3. Which one of the following numbers is divisible by 7
   5894, 56723, 17259
4. Is 2353740 divisible by 4?
5. Which one of the following numbers is divisible by both 2 and 5?10002, 453970, 637385
6.  A number is divisible of 2 and 3, will it be divisible by 5?
7. If a number is divisible by 2 only, will it be divisible by 4?
8. Which of the following numbers is divisible by 3?
   45769, 25784, 2391
9. List any three 3-digit numbers that are divisible by 5.
10. List two 4-digit numbers that are divisible by 4.

[/am4show]

This is not only a neat trick but a very practical skill - you can figure out the day of the week of anyone's birthday.

If you were born in the 20^th Century, (1900-1999), we can use math to find out which day of the week you were born. If you’re a little too young for this, try it with a parent or grandparent’s birthday. Watch the video and I'll teach you exactly how it works.

[am4show have='p8;p9;p11;p38;p92;p154;' guest_error='Guest error message' user_error='User error message' ]

Download Student Worksheet & Exercises

Did it work?  You can check via the Time and Date website, or simply do an internet search for the year and the word calendar, such as, “1996 calendar.”

Note: the codes shown in the video are special just to the years in the 1900s. If you'd like to be able to expand this to other centuries, you'll need to use the codes listed below and learn how to shift them (like I did for you in the video).

What about years 2000-2099?

The general formula is: Month Code + Date + Year Code - (biggest multiple of seven).

For Nov. 18, 2006 = 2 + 18 + 0 = 20.

20 - (7 * 2) = 20 / 14 = 6 so Nov 18, 2006 is on a Saturday using the codes below! (Do you notice how the following codes are different than they were for 1900s?)

Day Codes:

• Sunday = 0
• Monday = 1
• Tuesday = 2
• Wednesday = 3
• Thursday = 4
• Friday = 5
• Saturday = 6
• Sunday = 0 or 7

Month Codes:

• January = 6*
• February = 2*
• March = 2
• April = 5
• May = 0
• June = 3
• July = 5
• August = 1
• September = 4
• October = 6
• November = 2
• December = 4

*For leap years (2000, 20004, 2008, 2012, 2016...) the code for Jan = 5 and Feb = 1.

Year codes:

• 2000 = 0
• 2001 = 1
• 2002 = 2
• 2003 = 3
• 2004 = 5
• 2005 = 6
• 2006 = 0
• 2007 = 1
• 2008 = 3
• 2009 = 4
• 2010 = 5
• 2011 = 6
• 2012 = 1
• 2013 = 2
• 2014 = 3
• 2015 = 4
• 2016 = 6
• 2017 = 0
• 2018 = 1
• 2019 = 2
• 2020 = 4
• 2021 = 5
• 2022 = 6
• 2023 = 0
• 2024 = 2
•  2025 = 3

We don't have to memorize 2000-2099 because we know how to divide numbers since the table repeats itself.

Here's how it works: if you need the code for 2061, divide 61 by 4 to get 15 (with a remainder of 1 that we ignore), so 2061 has a year code of 61 + 15 = 76. Don't forget to subtract out any multiple of 7, so we get 76 - 70 = 6. The year code for 2061 is 6!

This works the same way for the 1900s: Fir December 3, 1998 we have 98 divided by 4 which gives 24 (with a remainder of 2 that we ignore), so 1998 has a year code of 98 + 24 + 1 = 123. Now subtract out the biggest multiple of seven (which is 119) to get 123 - 119 = 4. 1998 has a year code of 4!

What about year codes for other centuries?

Did you notice how I added "1" to the year code in the previous example? That's because I had to shift it over since it's in the 1900s. For the 1800s we'd shift it by 3. Let me show you how:

Abraham Lincoln's birthday is Feb 12, 1809. 2009 has a year code of 4, that we need to add 3 to (this is the shift by 3), so we get 7 (which reduces down to zero). The year code for 1809 is 0.

So, his birthday is: 2 + 12 + 0 - 14 - (biggest multiple of seven) = 14 - 14 = 0.

Lincoln was born on a Sunday!

For 2100 dates, you'd need to add 5 to the year code (or subtract 2 from the year code). For example, 2109 has a year code of 4 + 5 = 9. Subtract out 7 gives a year code of 2. For 1700s, you'll treat them just like the 2100s.

Why does this work?

We're using a Gregorian calendar. While this type of calendar was created in 1580s, it wasn't until Wed, Sept 2, 1752 when it was adopted by England and American colonies. 1752 has a year code of zero. Which is why this method won't work for any dates before this, as they were on the Julian calendar. Note that the Gregorian calendar repeats itself every 400 years, so you can convert any future date into a date near 2000. For example, March 19, 2361 and March 19, 2761 will both be on a Sunday.

Exercises

Identify the days corresponding to the following dates given in the format,: mm/dd/yyyy

1. 11/16/1997
2. 1/1/1997
3. 05/27/1995
4. 08/15/1997
5. 07/15/1977
6. 03/01/1977
7. 11/24/1974
8. 06/27/1958
9. In a certain family, Janet was born on May 20, 1992 while Lewis was born on March 31, 1996. Who was born on Sunday?
10. On which day is April 30, 1960?

[/am4show]

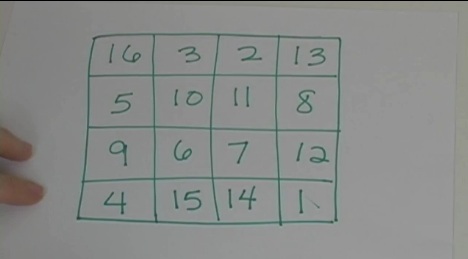
Magic squares have been traced through history as known to Chinese mathematicians, Arab mathematicians, India and Egypt cultures. The first magic squares Magic squares have fascinated people for centuries, and historians have found them engraved in stone or metal and worn as necklaces. Early cultures believed that by wearing magic squares, it would ensure they had long life and kept them from getting sick.

Benjamin Franklin was well-known for creating and enjoying magic squares, and it was all the rage during his time. Here's the deal: we're going to arrange numbers in a way so that all the rows, columns, and even the diagonals add up to a single number (called a Magic Sum). In this video, I show you the first Magic Square published in Europe way back in 1514. Plus, I show you how to make your very own Magic Square. You can use it to test your friends.

[am4show have='p8;p9;p11;p38;p92;p154;' guest_error='Guest error message' user_error='User error message' ]

Download Student Worksheet & Exercises

You can create a magic square that sums to any number by referencing the original "34" magic square. Ask a friend for a number larger than 34 (which is the smallest magic square you can create), and then follow these easy steps:

1. First take the number your friend gave you and subtract 34.
2. Divide your number from #1 by 4 and keep the remainder to use like this: the quotient is the first magic number and the quotient plus the remainder is the second magic number. For 67 the results are 8 and 9.
3. When you fill out a square in your new 4x4 magic square, peek at the 34-magic-square and see what's already in the box. If it's a 13, 14, 15, or 16, then add the second number to it and put it int he box. If not, add the first number to it.

Note that if your number is even (but not a multiple of 4) then you'll have the same number for your first and second numbers. That's okay!

Exercise

Find the value of the letters; A, B,C and D in the following upside-down magic square

1. A
2. B
3. C
4. D
5. What is the sum of elements of any diagonal in the first magical square published in 1514?
6. Find the element at the middle of a nine-element magic square.
7. Draw a nine-element magic square.

Find the values of b and c in the following magic square.

8. b
9. c
10. d

[/am4show]

Have you ever heard of a dollar word search? It’s a special kind of puzzle where the letters in a word add up to a coin value. For example, an A is worth a penny, the letter B is worth two cents, C is worth three cents, and so on. Are you completely confused? That's okay!  Just watch the video and I’ll show you how it all works.

[am4show have='p8;p9;p11;p38;p92;p154;' guest_error='Guest error message' user_error='User error message' ]

Download Student Worksheet & Exercises

Were you able to use my hints to find some dollar words? Keep trying! It’s really fun and rewarding to find out which words work. Please add a comment below if you discover a new one. We would love to add it to our growing list of dollar words!

Exercises

1. What is the word “bucket” worth?
2. Determine the monetary value of the word “toilet.”
3. What is a “starfish” worth?
4. The shortest sentence in English is “Go.” How much is it equivalent to?

Which one of the following has the greatest monetary value?

1. Supper, dinner, lunch
2. Monday, Sunday, Tuesday

[/am4show]

This is a neat trick that you can use to really puzzle your friends and family. If someone gives you a three-digit number, you can actually figure out what the end result will be after you've received two additional numbers, but before you actually know what those numbers are. Does this sound confusing?  Watch the video and I’ll show you how it works.

[am4show have='p8;p9;p11;p38;p92;p154;' guest_error='Guest error message' user_error='User error message' ]

Download Student Worksheet & Exercises

Were you able to figure this problem out? The real trick is that you’re simply adding 1,998 to the first number that you received. No matter which other two numbers are given to you, make sure the number you write down makes each pair of numbers' sum 999. If you do this correctly twice, then the row of numbers you add together will be the same as the initial number plus 1,998. Try it out and let me know if it works for you!

Exercises

Predict the end result for the following numbers:

1. 235
2. 988
3. 002
4. 999
5. 427
6. 777
7. 559
8. What would be the difference between a number 769 and its predicted result based on the above knowledge?
9. A mathematician was given a number x and gave its end result as 2877. What is the value of x?
10. Suzanne was asked by her friend to predict the end results of 932 within a few seconds. If she was given 432 as one of the two additional numbers to complete the proof of the predicted number, which number did she write immediately afterwards?

[/am4show]

Numbers really can be huge – some are too big to even imagine!  Have you ever seen a million pieces of candy? Or have you ever even tried to count to one million? In this video, we’ll try to figure out about how long it would take just to count to one million. I’ll also show you how to write some really big numbers!

[am4show have='p8;p9;p11;p38;p92;p154;' guest_error='Guest error message' user_error='User error message' ]

Download Student Worksheet & Exercises

So there are 31,536,000 seconds in a year, but you couldn’t spend all of your time counting. Simply saying larger numbers will take much longer than a second! So with lots of breaks for sleeping, eating, and homework, it would take more than a year to count to a million…and most people get bored with counting way before that.

Exercises

1. How many seconds are there in one hour?
2. How many seconds are there in a day?
3. How many days does a leap year have?
4. Write a number greater than but closer to a billion.(Note the difference between the two should be less than 50)
5. Write a number lesser than but closer to a billion.(Note the difference between the two should be less than 50)

Write the following numbers out numerically:

1. A thousand billion
2. A thousand million
3. A hundred hundred
4. Write a number that is 1 less than 100,000,000,000

[/am4show]

Have you ever heard someone refer to a “million billion” of something? Is that more or less than a “billion million?” In this video, I’ll show you how to write down these numbers and figure out which one is larger.

[am4show have='p8;p9;p11;p38;p92;p154;' guest_error='Guest error message' user_error='User error message' ]

Download Student Worksheet & Exercises

Did one of these numbers sound bigger to you? To me, they’re both a strange way to say the exact same number – which is actually a quadrillion!

Exercises

Write out each number long-ways (with all the zeros written out):

1. A thousand million
2. A thousand billion
3. Ten million
4. A hundred billion

Write the exponential form (ten and a superscript) of the following numbers

5. A thousand million
6. A thousand billion
7. Ten million
8. A hundred billion

Determine the exponents of the following number if written in the form; ”ten and a superscript.”

9. 10,000,000,000
10. 100

[/am4show]

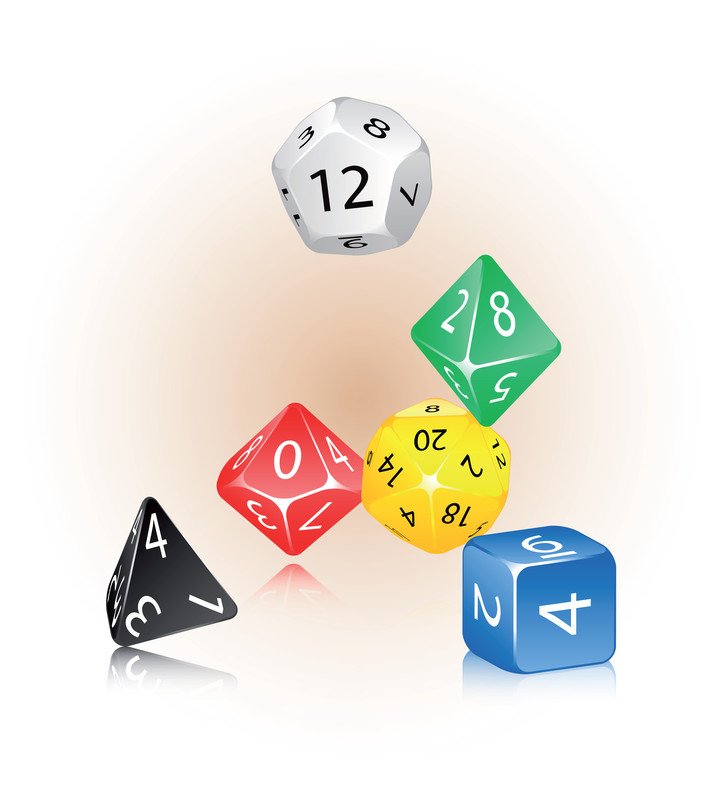
Did you know I carry a set of dice in my pocket just for this game? It's as old as the hills and just as fun to play now as it was when I was a little math whiz back in 2nd grade.  (No kidding - when we had 'math races', I was always team captain.  Not quite the same thing as captain on the soccer field, though...)

This is one of those quick-yet-satisfying dice games you can play to hone your thinking skills and keep your kids busy until the waiter arrives with your food.  All you need are five or six standard 6-sided dice and two 12-sided dice.  (Note - if you can't find the 12-sided dice, just skip it for now.  You can easily substitute your brain for the 12-sided dice.  I'll show you how.)
[am4show have='p8;p9;p11;p38;p92;p154;' guest_error='Guest error message' user_error='User error message' ]

You need to do two things to play this game. You can use a calculator with this game, but usually the kids without the calculator win the round, as it usually takes longer to punch in the numbers than figure out the different possibilities in your head (and that's what you're working on, anyway!) If  your kid is a highly visual learner, then hand them a scratch pad and a pencil so they can scribble down stuff as they go.

Download Student Worksheet & Exercises

First, roll the two 12-sided dice. Multiply the two numbers in your head.  If you rolled a 6 and 6, you'd now have 36. That's your target number.  If you don't have the 12-sided dice, just think up two numbers, each between 1 and 12 and use those.

Next, roll the 6-sided dice. Now, using your arithmetic skills, figure out a way to add, subtract, multiply or divide those three numbers to get the number you rolled with the first set.  So if you rolled six 6-sided dice and got 4, 5, 2, 1, 1, 5, you could do this:

(Red numbers are the ones rolled on 6-sided dice.)

(4 x 5) - 2 = 18

18 x (1 + 1) = 36

You don't have to use all the numbers, but you can't double up and use a 4 twice if you only rolled one 4.  And that's it!  It's loads of fun and engaging, because it's got more than one answer.  And sometimes there's no answer (although rarely!). As you get faster and better at this game, try taking away one or two of the dice.  It's more challenging.

HOT TIP: You can add in the use of exponents when your kids get the hang of the game. An exponent tells you how many times to multiply a number by itself. For example, a 2 with a 3 exponent looks like: 2³ = 2 x 2 x 2 = 8. To use exponents, simply use one of the numbers as an exponent. For example, if you rolled five 6-sided dice and got 5, 2, 3, 2, 4, you can do this to get 36 (given 36 came from the 12-sided dice):

(Red numbers are the ones rolled on 6-sided dice.)

(5 x 2) = 10² = 100

100 - (4³) = 36

When your kids get good, you can up the ante and use a set similar to what I have in my purse: one 20-sided double dice and a handful of 6-sided. Math craze, anyone?

Exercises

No dice? Try these combinations that I rolled and recorded for you. I rolled six 6-sided dice and two 12-sided dice. Can you figure out a combination that would make each target number? Remember that the target number is the product (multiplication) of the two numbers from the 12-sided dice.

6-sided dice               12-sided dice

1. 2,3,5,6,1,3         ---     10,2
2. 4,3,6,4,5,3         ---     12,9
3. 1,6,4,4,2,1         ---     5,8
4. 4,1,1,1,2,3         ---     3,9
5. 1,6,6,5,5,1         ---     9,7
6. 2,1,4,5,2,2         ---     6,3
7. 3,1,6,5,4,1         ---     11,4
8. 4,3,6,4,5,3         ---     12,7
9. 2,2,3,3,4,6         ---     4,6
10. 3,5,6,1,3,3         ---     6,9

[/am4show]

Here's our first MATH lesson. It is so easy that one night, I wound up showing it to everyone in the pizza restaurant. Well, everyone who would listen, anyway. We were scribbling down the answers right on the pizza boxes with such excitement that I couldn't help it - I started laughing right out loud about how excited everyone was about math... especially on a Saturday night.

When you do this calculation in front of friends or family, it's more impressive if you hand a calculator out first and let them know that you are 'testing to see if the calculator is working right'.  Ask for a two digit number and have them check the calculator's answer against yours.

If you really want to go crazy, you can have math races against the calculator and its operator, just as the Arthur Benjamin video shows.  (Only you don't need to do the squaring of five-digit numbers in your head!)  Have fun!
[am4show have='p8;p9;p11;p38;p92;p154;' guest_error='Guest error message' user_error='User error message' ]

Download Student Worksheet & Exercises

So here's the deal:

11 x 23 = ?

Take the 23 and spread it apart, so it looks like "2 3" with a space in the middle. Now add 2 + 3 to get: 2 + 3 = 5 and insert the 5 into the space. So...

11 x 23 = 253

That's it. How cool is that??

What about this one? 11 x 45 = ?

Spread apart the 4 and 5, then insert the sum of the 4 and 5 in between to get:

11 x 45 = 495

Whoa...!!! This stuff is soo cool! But wait a second... you hit a speed bump when you try this one:

11 x 86 = ?

It seemed a bit ridiculous to get: 11 x 86 = 8146. The answer should be a 3-digit number, not 4! So, check again and then find that you need to 'carry' the one to the first digit, so it becomes:

11 x 86 ==> 8(14)6 ==> = 946

And of course, if you can do 86, you have to give 99 a try:

11 x 99 ==> 9(18)9 ==> 1,089

Now you give yourself a few different numbers to try. Check your answer with a calculator!

Tell me how YOU think this works in the comment field below!

Exercises

1. 11 x 11
2. 11 x 27
3. 11 x 43
4. 11 x 49
5. 11 x 50
6. 11 x 67
7. 11 x 79
8. 11 x 89
9. 11 x 92
10. 11 x 96

[/am4show]

If you can multiply 11 by any 2-digit number, then you can easily do any three digit number. There's just an extra step, and make sure you always start adding near the ones so you can see where to carry the extra if needed.
[am4show have='p8;p9;p11;p38;p92;p154;' guest_error='Guest error message' user_error='User error message' ]

Click the player to learn how to multiply any three-digit number by eleven:

Download Student Worksheet & Exercises

Tell me how YOU think this works in the comment field below!

Exercises

1. 11 x 163
2. 11 x 235
3. 11 x 345
4. 11 x 479
5. 11 x 659
6. 11 x 748
7. 11 x 997
8. 11 x 982
9. 11 x 873
10. 11 x 769

[/am4show]

Squaring three-digit numbers is one of the most impressive mental math calculations, and it doesn't take a whole lot of effort after you've mastered two-digits. It's like the difference between juggling three balls and five balls. Most folks (with a bit of practice) can juggle three balls. Five objects, however, is a whole other story (and WOW factor).

Once you get the hang of squaring two-digit numbers, three-digit numbers aren't so hard, but you have to keep track as you go along. Don't get discouraged if you feel a little lost. It's just like anything you try for the first time... when you're new at something, in the beginning you aren't very good at it. But with practice, these steps will become second nature and you'll be able to impress your friends, relatives, and math teachers.

The video below has two parts:

[am4show have='p8;p9;p11;p38;p92;' guest_error='Guest error message' user_error='User error message' ]

Download Student Worksheet & Exercises

Exercises

1. 〖93〗^2
2. 〖193〗^2
3. 〖979〗^2
4.  〖249〗^2
5. 〖415〗^2
6. 〖84〗^2
7. 〖573〗^2
8. 〖333〗^2
9. 〖757〗^2
10. 〖696〗^2

[/am4show]