When most people think of waves, they imagine something like an ocean wave… it moves through the water and isn’t confined to one area. Some waves don’t travel at all – they are called standing waves.
[am4show have=’p9;p58;’ guest_error=’Guest error message’ user_error=’User error message’ ]
Picture two waves traveling in opposite directions. One is going to the right, the other going to the left. What happens when they combine? Using superposition, we can figure out what the interacting waves look like when they interfere with each other.
Did you notice how there are places along the string where the string is not moving at all? It’s at permanent rest… it’ doesn’t vibrate at all. Those places are called nodes. The places where the amplitude is greatest is called the antinodes.
Click here to go to next lesson on Nodes and Antinodes.
[/am4show]
One common misconception is the idea that noes and antinodes are the same as the crest and trough of a wave. They’re not. A node is a place on the wave that is permanently at rest. An antinode is where the wave is at its maximum (it will travel through a large up and a large down displacement).
[am4show have=’p9;p58;’ guest_error=’Guest error message’ user_error=’User error message’ ]
You’ll find standing waves when you look at columns of vibrating air or strings vibrating at resonance. This happens because of two things going on simultaneously: when the wave hits the barrier, instead of continuing on, it gets reflected back.
The reflected wave constructively interferes with the next incoming waves, and the overall effect is that you have places on the string that never move and places where it’s always at a maximum. This effect is what we call a standing wave.
Nodes and antinodes aren’t really part of the wave because a standing wave really isn’t a wave at all… it’s just a visual effect that looks like a wave that doesn’t move. You have to perfectly time the interference of two (or more) opposite-traveling waves to get this effect.
Click here to go to next lesson on Simple harmonic motion.
[/am4show]
Standing waves are basically two waves traveling in opposite directions that constructively interfere with each other so it looks like the whole system is moving in simple harmonic motion.
[am4show have=’p9;p58;’ guest_error=’Guest error message’ user_error=’User error message’ ]
Simple harmonic motion is when we used Hooke’s Law for the mass-spring system to figure out the displacement, period, or frequency of the system.
First harmonics have 2 nodes and 1 antinode. Second harmonics have 3 notes and 2 antinodes, third harmonics have 4 nodes and 3 antinodes, and so on.
Click here to go to next lesson on Build a Standing Wave Machine.
[/am4show]
Standing wave machines are fun to make because they are easy to build and amazing to watch! Here’s a simple one you can make on your own using the materials from the previous lessons in electricity.
[am4show have=’p9;p58;’ guest_error=’Guest error message’ user_error=’User error message’ ]
Materials:
- AA batteries (4, cheap “dollar-store” carbon-zinc kind work great)
- AA battery case (4)
- Alligator clip leads
- DC, 3V motor (2)
- Hot glue gun (and glue sticks)
- Masking tape
- Popsicle sticks
- String
- Scissors
How many wavelengths can you see in yours? Where are the nodes and antinodes? Change the tension in the strong to get different harmonics to show up! (Note – if you know how to change the motor speed using a potentiometer, you can do that also!)
Also note – if you’re finding that the string wads into a tight ball after only a few seconds, it means that one of your motors is going the wrong direction. Stop both motors and switch the wires in the back of ONE of the motors to reverse the polarity (plus and minus) so the motor spins in the opposite direction. You want the one motor to wind up the string and the other to un-wind it at the same time. Eventually, since the motors spin at slightly different speeds, the string will get wound up and you’ll need a new piece of string.
Click here to go to next lesson on Standing Wave Math.
[/am4show]
It’s easy to calculate the frequency, period, wavelength and speed of waves at different harmonics.
[am4show have=’p9;p58;’ guest_error=’Guest error message’ user_error=’User error message’ ]
For a tight string, there’s a handy equation that we can use to relate the length of the string to the wavelength based on the harmonic number like this:
L = (n/2) λ
where L is the length of the string, and n is the harmonic number. Here’s how to use this equation to find everything we need about the wave:
You’ve finished this section! Now it’s your turn to do physics problems. Click here to download your homework problem set.
[/am4show]
When a wave travels from one medium to another, like sound waves traveling in the air and then through a glass window pane, it crosses a boundary. Whether the wave continues to the new medium (and even how it goes through), or whether it bounces and reflects back, or a bit of both depends on the boundary.
[am4show have=’p9;p58;’ guest_error=’Guest error message’ user_error=’User error message’ ]
Imagine a jump rope attached to a door handle. The last particle of the rope is fixed tot he door handle, and doesn’t move at all. If you grab the free end of the rope and pull it taught, you have a nice, straight line. When you jerk the rope up, the pulse travels through the rope toward the door handle. Some of the energy carried by the pulse is reflected and comes back to you at the same speed and wavelength, but it’s upside down (called a reflected pulse) and not as large amplitude-wise. Some of the energy is also transmitted to the fixed end, causing the door handle to rattle and vibrate.
If you untie the rope from the door handle and instead tie it loosely to a pole (so it’s allowed to slide up and down easily) and repeat this experiment, you’ll find the pulse travels through the rope, turns around and reflects back right side up with the same speed and wavelength.
Now imagine untying the rope and instead attaching a rope denser, thicker rope to the end. The initial pulse travels toward the thicker rope, but two tings happen when it hits the thicker rope: first, a reflected pulse (same speed and wavelength, but inverted) returns back to you, but also some of the energy goes into the thicker rope so a smaller, slower wave (but with the same frequency as the original pulse) will travel along the thicker rope. Waves travel fastest in the least dense medium, so the reflected wave travels faster than the transmitted wave. Even though the waves travel at different speeds in different mediums, they are all vibrating with the same frequency.
What would you expect to happen if a sound wave traveled from the denser rope to a less dense rope? The initial pulse (also called the incident pulse) travels through the denser medium, and when it hits the lesser dense rope, it undergoes partial transmission and partial reflection like this: the reflected pulse has the same speed and wavelength (and is right side up). Second, the wave transmitted to the less dense rope is right-side up, larger amplitude, and traveling faster than the reflected pulse.
The bottom line? Waves travel fastest in the least dense medium. Frequency doesn’t change when you cross a boundary. The wavelength is always greatest in the least dense rope. The amplitude is always greatest in the initial (incident) wave.
The reflected wave inverts when it moves from a less dense to a more dense rope due to Newton’s Laws of Motion. For the case when the rope is free to slide up and down on the pole, when the initial wave reaches the pole, the rope slides up and because of its inertia, it overshoots and exerts a reaction force on the string, and this reaction force sends a reflected wave back down the string (called a soft reflection). With the case of being fixed on a door handle, when the incident wave reaches the end, it exerts an upward force on the door handle, but Newton’s Third Law states that there’s an equal and opposite (reaction) force that the door handle exerts on the string, which generates an inverted pulse that travels back along the string (called a hard reflection).
Click here to go to next lesson on Wave Reflection.
[/am4show]
Straight waves are what happens when something moves back and forth in a medium like water. These are interesting when they hit a diagonal plane barrier, because when the incident wave reaches the barrier, the waves always reflect at the same angle that they approached the barrier with (called the Law of Reflection).
[am4show have=’p9;p58;’ guest_error=’Guest error message’ user_error=’User error message’ ]
We’ll look at how waves reflect off curved surfaces(like a parabolic mirror) when we get to our section on light waves.
Click here to go to next lesson on Wave Refraction.
[/am4show]
Waves bend when they go from one medium to another when the speed changes. It’s a really important topic in light (not so much with sound), because it’s how lenses, eyes, cameras, and telescopes work. The bending of sound waves happens naturally in the air above the earth when it’s warmer than the surface of the earth. The sound waves that travel through the warmer air are faster and the ones that travel through cooler air are slower. When the sound waves go from warmer to cooler air (less dense to more dense air), they become bent back down toward the surface.
[am4show have=’p9;p58;’ guest_error=’Guest error message’ user_error=’User error message’ ]
So refraction can bend sound downward which in turn amplifies the sound by adding to the direct (original source) sound. If you’ve ever been near a cool lake, you’ve heard one of nature’s amplifiers!
But why does sound bend? You can imagine a toy car going from a wood floor to carpeting. One wheel hits the carpet first and slows down before the other, causing the toy to turn. The direction of the sound changes in addition to the speed. The slower speed must also shorten its wavelength since the frequency of the wave doesn’t change. Here’s the wave equation again from the previous section:
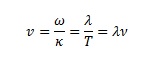
Note the first v is velocity, and the last ν is frequency in the equation.
Click here to go to next lesson on Diffraction.
[/am4show]
When waves pass around small (we’re talking small compared to the wavelength of the wave) objects, they diffract. People in the audience of a concert can hear really well if they are sitting right behind a pillar because the sound waves are large enough to bend around it (which is actually because of both diffraction and reflection effects). Diffraction helps sound bend around obstacles. You can sometimes hear conversations around corners because of diffraction.
[am4show have=’p9;p58;’ guest_error=’Guest error message’ user_error=’User error message’ ]
Waves also diffract if they spread out after moving through small (again, smaller than wavelength-size) openings, like light going through a slit cut with a razor.
The amount a wave diffracts (bends) depends on the wavelength. Lower frequencies bend around objects better than higher frequencies. If you’ve ever watched a lightning and thunder storm, you know that there’s a lot more sound (like a sharp crack) when the lightning is closer (you hear both higher and lower frequencies) than when it’s more distant (mostly lower frequencies). Owls use low frequency sounds to transmit sounds further than the higher frequency bird twitters.
Click here to go to next lesson on Superposition.
[/am4show]
Often two (or more) waves travel through the same spot. If you’ve ever listened to an orchestra, you’re hearing the sounds from many different instruments all playing at the same time. If more than two boats are on the lake, their wakes churn up the water together. Here’s how we handle this in physics…
[am4show have=’p9;p58;’ guest_error=’Guest error message’ user_error=’User error message’ ]
The principle of superposition states that when waves interfere with each other, the displacement at any location is the sum of the displacements of the waves at that location. Said another way, you simply add up the waves at the same spot to get the resulting amplitude.
Click here to go to next lesson on Interference.
[/am4show]
What if two waves of the same wavelength and amplitude travel in the same direction along a stretched string? What will the string look like? We know about the idea of superposition adding the waves together, but what does the string actually look like?
[am4show have=’p9;p58;’ guest_error=’Guest error message’ user_error=’User error message’ ]
How waves interact with each other depends on whether the waves are in phase or not. If they are in-step (in phase) with each other, then it’s easy to add up to double the displacement (constructive interference). If they are completely out of step, then they cancel each other out (destructive interference).
Click here to go to next lesson on Constructive Interference.
[/am4show]
When two waves have an increase in displacement when they interact, it’s constructive interference.
[am4show have=’p9;p58;’ guest_error=’Guest error message’ user_error=’User error message’ ]
Click here to go to next lesson on Destructive Interference
[/am4show]
Destructive interference happens when two waves have opposite displacements. The pulses don’t destroy each other (as the name implies), but rather they cancel out the effect of each other when they interact with each other.
[am4show have=’p9;p58;’ guest_error=’Guest error message’ user_error=’User error message’ ]
They don’t have to cancel each other out completely to be destructive interference. They don’t even have to have the same amplitudes. (And actually, when two waves meet, they don’t even alter their path or alter the waveform itself after the interaction. They simply add or subtract when they interact, and then go on their merry way as they had been before the interaction when they’re done. It’s really quite amazing.)
Click here to go to next lesson on Which kind of interference is it?
[/am4show]
In previous lessons we’ve learned that energy is the ability to do work, and that work is moving something a distance against a force. The concept of energy is fairly easy to see as far as lifting things or pushing things go. We are exerting energy to lift a box against the force of gravity. We are exerting energy to pedal our bike up a hill. But how does this energy stuff relate to light, electricity, or sound? What’s moving against a force there?
[am4show have=’p9;p58;’ guest_error=’Guest error message’ user_error=’User error message’ ]
With energy, what’s happening is that outrageously tiny particles are moving back and forth outrageously tiny amounts, at outrageously high speeds. With light, you’ve got little photons moving, with electricity little electrons. With sound, you’ve got molecules moving back and forth.
This back and forth motion is called vibration and these vibrations make waves. When one particle moves back and forth it does work on another particle, which does work on another particle and so on. As these particles do work on one another, they cause a wave to move from one place to another.
Energy moves by waves or, in other words, waves are energy-mobiles! Before we get in over our heads talking about waves however, we need to spend some time on this vibration thing.
If you imagine a swing at the park, it’s got a normal resting position (called an equilibrium position). That’s when it’s experiencing a balance of forces: the pull of gravity balances with the tension in the chain holding up the swing, and so forth. Everything adds up to zero, and stays at zero until a kid comes by.
When a kid starts pumping on the swing, the swing is no longer in equilibrium and the swing starts to move back and forth through an arc. This is a slow forced vibration that stops soon after the kid leaves the swing, and the kid needs to keep pumping back and forth to keep swinging at the same rate (or increase the swing rate). Eventually, the kid gets tired and stops pumping, and each repetition of the swing moving back and forth (vibration) is less and less (called damping). Eventually, the swing comes to a stop (equilibrium) until another energetic kid comes along.
Click here to go to next lesson on Damping.
[/am4show]
Let’s practice figuring out which interference is being observed when waves interact…
[am4show have=’p9;p58;’ guest_error=’Guest error message’ user_error=’User error message’ ]
Click here to go to next lesson on Doppler Effect.
[/am4show]
Damping is when a spring, swing, or other vibrating object loses its energy over time. It means that without adding energy into the system, like pumping on a swing or hitting a drum head, the object will eventually come to its non-vibrating (equilibrium) position.
Imagine the kid on the swing again. Why does the kid move past the equilibrium point without stopping?
[am4show have=’p9;p58;’ guest_error=’Guest error message’ user_error=’User error message’ ]
It’s actually because of Newton’s law of inertia. The swing continues on its path as long as there are balanced forces acting on it. As the swing moves past its equilibrium point, a restoring force acts on it to move it back to its original equilibrium position.
The difference between a vibration (like a kid swinging) and translational motion (like a kid on roller skates) is that the kid on skates can be permanently displaced from his starting position. The kid on a swing doesn’t move away from its original equilibrium position for long – it stops, turns around, and comes back due to the restoring force. An object that vibrates actually wiggles and jiggles around a fixed position (the equilibrium position).
Other examples of vibrating objects include tuning forks (which are like inverted swings), piano strings, car suspension systems, a weight on the end of a spring that bobs up and down, and drum heads. In each of these examples, when the object is disturbed (like hitting the tuning fork or drum head, or pulling the weight at the end of the spring), the object moves from its original resting position, stops and heads back toward its resting position and overshoots, stops and come back toward the resting position and the cycle repeats. The object moves along the same path over and over again, and if there was no friction or drag force (or other energy losses), the object would continue to move back and forth forever.
Did you notice that when you graph out the motion of the mass on a spring, it has a particular shape? The shape is described in math as a sinusoidal wave, or y = sin(x). Did you notice how it is periodic and that you could also see the damping effect? The damping effect means that energy is being lost or dissipated. (Scientists wouldn’t say that it’s slowing down, because that indicates that the speed is decreasing, which isn’t the case when the mass stops and turns around to head back to the resting position.. it is actually speeding up!)
Click here to go to next lesson on Frequency.
[/am4show]
The concept of frequency is very important to understanding energy. When it comes to electromagnetic waves it is frequency that determines whether the wave is radio, light, heat, microwave or more. It’s all the same type of energy, it’s the frequency that determines what that energy actually does. With sound energy the frequency determines the pitch of the sound.
[am4show have=’p9;p58;’ guest_error=’Guest error message’ user_error=’User error message’ ]
As we move forward with energy, it is quite important that you know that all waves come from some sort of vibrating particle somewhere. The reason you can pick up a signal on your radio is because somewhere, maybe miles away, there is a particle vibrating at some ridiculous speed, creating a wave that moves across distances to finally vibrate the particles inside your radio’s antenna. It’s important to realize, however, that the particle does not move over that distance. The particle that started the wave back at the radio station is still there. It did not move to your radio it just vibrated at the antenna and started the wave.
Frequency is a measure of how many times something moves back and forth. A swing, a pendulum, a leg of a walking person all have a frequency. All those things start at one place, move, and come back to the same position that they started. This moving and coming back is one vibration. The faster something vibrates, the more frequency that something has.
Frequency is measured in Hertz. One Hertz (or Hz for short) is one vibration in one second. The Hertz is named after Heinrich Rudolf Hertz (1857-1894) a German physicist and professor. Hertz proved that electricity can be transmitted in electromagnetic waves, which travel at the speed of light and which possess many other properties of light. His experiments with these electromagnetic waves led to the development of the wireless telegraph and the radio.
A Hertz is a relatively slow vibration so there are also kilohertz (KHz), megahertz (MHz), and gigahertz (GHz). A kilohertz is 1000 Hz, a megahertz is 1,000,000 (a million) Hz, and a gigahertz is 100,000,000 (one thousand million) Hz.
In this experiment you will be adjusting the length of string of a pendulum until you get a pendulum that has a frequency of .5 Hz, 1 Hz and 2 Hz. Remember, a Hz is one vibration (or in this case swing) per second. So .5 Hz would be half a swing per second (swing one way but not back to the start). 1 Hz would be one full swing per second. Lastly, 2 Hz would be two swings per second. A swing is the same as a vibration so the pendulum must move away from where you dropped it and then swing back to where it began for it to be one full swing/vibration.
You’ll need:
- 3 Foot Long String
- A Weight that can be tied to the end of the string
- A Timer or Stopwatch
- Masking Tape
- A Table or Chair
- A Partner is helpful
“Advanced students: Download your What is Frequency?”
1. Tie your weight (the official name of the weight on the end is bob. Personally I’ve always preferred the name Shirley, but Bob it is.) to the end of the 3 foot string. If you’ve done the gravity lesson in the Mechanics set of lessons you’ll remember that the weight of the bob doesn’t matter. Gravity accelerates all things equally, so your pendulum will swing at the same speed no matter what the weight of the bob.
2. Tape the string to a table or chair or door jam. Make sure it can swing freely at about 3 feet of length.
3. I would recommend starting with 1 Hz. It tends to be the easiest to find. Then try .5 Hz and then 2 Hz.
4. The easiest way I’ve found to do this is to start the pendulum swinging and at the same time start the timer. Count how many swings you get in ten seconds.
5. Now, adjust the string. Make it longer or shorter and try again. When you get 10 swings in 10 seconds you got it! That’s one swing per second. You should be able to get quite close to one swing per second which is 1 Hz.
6. Now try to get .5 Hz. In this case you will get 5 swings in ten seconds when you find it. (A little hint, the string is pretty long here.)
7. Now speed things up a bit and see if you can get 2 Hz. Be prepared to count quick. That’s 2 swings a second or 20 swings in 10 seconds! (Another little hint, the string is quite short for this one.)
Did you get all three different frequency pendulums? It takes a while but my classes found it rather fun. You’ve created three different frequencies. 2 Hz being the fastest frequency. That was pretty fast right? Can you imagine something going at 10 Hz? 100 Hz? 1,000,000 Hz? I told you things were moving at outrageous speeds!
Some examples of things that work at these frequencies are AM radio stations which broadcast at KHz, FM stations which broadcast at MHz, and microwaves which cook your food with GHz. If your radio is “crankin” tunes from radio station 750 AM, a part of your radio is vibrating at 750,000 times a second. If you’re “pumping wattage into your cottage” with WSCI at 94.2 on your radio dial, a part of your radio is vibrating at 94,200,000 times a second. If your radio happens to be green, then light is vibrating off your radio at 6 x 1014 Hz. That’s 6 with 14 zeros behind it or 600,000,000,000,000 vibrations in one second. That’s some serious vibes!
(By the way, if you can hear the sound coming out of your radio, your speakers are vibrating anywhere between 20 and 20,000 Hz. See how vibrations are important? They’re everywhere!) Let’s look more carefully at what those vibrations make, and that’s waves.
Click here to go to next lesson on Period.
[/am4show]
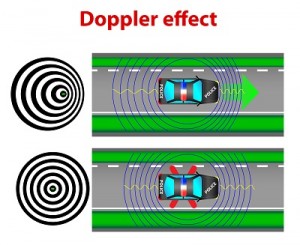Imagine a police car on the side of the road with lights and sirens on full blast. You’re also parked and you hear the same frequency (say 1,000 Hertz) of the siren. However, if you’re driving at 75 mph toward the police car. you’re going to hear a higher frequency (1096 Hz), and if you’re driving away at 75 mph, you’re going to hear a lower frequency of 904 Hz. Why is that?
[am4show have=’p9;p58;’ guest_error=’Guest error message’ user_error=’User error message’ ]
It has to do with a motion-related frequency change called the Doppler Effect. This effect was initially conceived by Johann Doppler in 1842 and later tested by Buys Ballot in Holland in 1845 with a locomotive drawing an open car with trumpeters. There’s Doppler Effect for not only sound but also light including microwaves, radio waves, and visible light. Police use the Doppler Effect on their radar guns to track your speed. Astronomers use it to find the motions of stars, galaxies, and quasars… it’s really an amazing tool in our scientific toolbox!
Click here to go to next lesson on Standing Waves.
[/am4show]
The period is the time it takes for one full cycle to complete itself and is measured in seconds per cycle. The frequency is the number of cycles that are make in a period of time, and is measured in cycles per second.
[am4show have=’p9;p58;’ guest_error=’Guest error message’ user_error=’User error message’ ]
Click here to go to next lesson on The Frequency and Period Relationship.
[/am4show]
The frequency is the number of cycles that are made in a given period of time, like 10 swings in 5 seconds, and is measured in cycles per second. The period is the inverse of the frequency, given by this equation: T = 1/ν.
[am4show have=’p9;p58;’ guest_error=’Guest error message’ user_error=’User error message’ ]
Click here to go to next lesson on Amplitude.
[/am4show]
Amplitude is how high or low the wave is from its original equilibrium position. (not vibrating). How high can you get the swing to go? How far does the car system spring travel over that bump? All these are the amplitude of the vibration.
[am4show have=’p9;p58;’ guest_error=’Guest error message’ user_error=’User error message’ ]
Let’s try a sample problem for amplitude:
Click here to go to next lesson on Pendulums.
[/am4show]
The restoring force slows down the object as it moves from its resting but speeds it up when it heads back to the resting position, and that’s what creates the vibration. We’re going to take a look at the forces in a pendulum from the point of view of Newton’s Laws.
[am4show have=’p9;p58;’ guest_error=’Guest error message’ user_error=’User error message’ ]
Click here to go to next lesson on Energy and Vibration.
[/am4show]
There’s more than one way to solve physics problems… and by looking at the total mechanical energy of the system, you’ll be able to solve much more complicated pendulum problems with ease.
[am4show have=’p9;p58;’ guest_error=’Guest error message’ user_error=’User error message’ ]
Click here to go to next lesson on Pendulum Period.
[/am4show]
You’ll need a pendulum for this experiment. A pendulum is really nothing more than a weight at the end of something that can swing back and forth. The easiest way to make one is to get a string and tape it to the edge of a table. (The string should be long enough so that it swings fairly close to the ground.) Tie a weight to the bottom of your string and you’ve got a pendulum.
[am4show have=’p9;p58;’ guest_error=’Guest error message’ user_error=’User error message’ ]
Now, for YOUR part of the experiment we are going to change one of three different things, and only one thing changes at a time. First, we’ll change the length of string and measure the period. Then we’ll change the mass of the object, and then the angle that you start the pendulum from. With each trial you will be changing only ONE of those three things. (The rest of the variables will be constant.)
- Make an observation. Play with the pendulum a bit and see how it behaves.
- Make a hypothesis. How will the length of string effect the number of swings in 10 seconds? Will there be more, less, or no change in the number of swings as the string gets shorter.
- Set a timer for 10 seconds or get someone who has a watch with a second hand to tell you when 10 seconds are up.
- Now for the test. Pull the pendulum back as far as you’d like (the pendulum swings smoother if you don’t lift the weight higher than the top of the string).
- Start the timer and let go of the weight at the same time.
- Count the swings the pendulum makes in 10 seconds. This is your frequency in #cycles per 10 seconds.
- Write down what you found (collect the data as shown in the video).
- Do two more trials with the string at that same length.
- Now change the changing variable. In other words, shorten the string. I would recommend shortening it at least an inch.
- Redo steps 3 through 9, recording each time.
- Continue shortening the string and doing trials until you get at least five different lengths of string.
- Convert frequency to period by taking the inverse. Do this for each trial.
Now report your results. Take a look at your data and see if you find a trend. Do you get more swings as the string shortens, less swings, or does the length of the string matter? Something interesting to notice is that at a certain length you will get 10 swings in 10 seconds or a swing a second. This is why pendulums are used in grandfather clocks. They keep good time!
Click here to go to next lesson on Hooke’s Law.
[/am4show]
How are pendulums like springs? They both vibrate, but how you model them on paper is a little different. Let’s take a look at how you handle springs and what their periodic nature looks like:
[am4show have=’p9;p58;’ guest_error=’Guest error message’ user_error=’User error message’ ]
Click here to go to next lesson on Nature of a Wave.
[/am4show]
Since we can’t see soundwaves as they move through the air, we’re going to simulate one with rope and a friend. This will let you see how a vibration can create a wave. You’ll need at least 10 feet of rope (if you have 25 or 50 feet it’s more fun), a piece of tape (colored if you have it), a slinky, and a partner. Are you ready?
[am4show have=’p8;p9;p16;p43;p64;p75;’ guest_error=’Guest error message’ user_error=’User error message’ ]
1. Give one end of the rope to your partner.
2. Stretch the rope out so that it is a bit slack.
3. Now move your hand up and down. Feel free to do it several times in a row. Your partner should keep his or her hands as still as possible.
4. Watch the waves move from your hand to the other end of the rope.
5. Now let your partner create waves.
6. If you wish, you can try to time your vibrations and create waves with specific frequencies. A frequency of one Hertz is fairly easy to do (one rope shake per second). Can you create rope waves of higher frequencies? You may find that your arm gets tired pretty quickly!
Your hand is the vibrating particle. As your hand vibrated up and down, you moved the particles of the rope up and down. As those particles of rope vibrated, they vibrated the particles next to them. As they vibrated, they vibrated the particles next to them and so on and so forth. So the wave moved from your hand across the room. Did your hands move across the room. Nope, but the wave you created with your vibrating hand did.
This is the way energy travels. Why is the rope wave energy? Because the particles moved a distance against a force. Work was done on the particles. In fact, when you shook the rope, your energy from your body moved across the room with the wave and was transferred (moved to) your partner. Your partner’s hands could feel the energy you put into the rope in the first place. The work you did on the rope was transferred by the rope wave and did work on your partners hand. You have moved energy across the room!
Now… let’s add another element to this experiment…
Transverse Waves
1. Put a piece of (colored if possible) tape in about the middle of the rope.
2. Tie your rope to something or let your friend hold on to one end of it.
3. Now pull the rope so that it is a bit slack but not quite touching the floor.
4. Vibrate your arm. Move your arm up and down once and watch what happens.
5. Now, vibrate your arm a bunch of times (not too fast) and see the results. Notice the action of the tape in the middle of the rope.
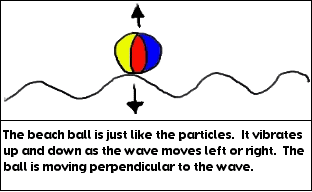What you’ve done is create a transverse wave. With a transverse wave, if the particle (in this case your hand) moves up and down, the wave will move to the left and/or right of the particle. The word perpendicular means that if one thing is up and down, the other thing is left and right. A transverse wave is a wave where the particle moves perpendicular to the medium. The medium is the material that’s in the wave. The medium in this case is the rope.
For example, in a water wave, the medium is the water. Your hand moved up and down, but the wave created by your hand moved across the room, not up. The wave moved perpendicular to the motion of your hand. Did you take a look at the tape? The tape represents a particle in the wave. Notice that it too, was going up and down. It was not moving along the wave. In any wave the particles vibrate, they do not move along the wave.
Longitudinal Waves
Now that you’ve seen a transverse wave, let’s take a look at a longitudinal wave. Here’s what you do:
1. Put a piece of tape on one slinky wire in the middle or so of the slinky.
2. Let your friend hold on to one end of the slinky or anchor the slinky to a chair or table.
3. Now stretch the slinky out, but not too far.
4. Quickly push the slinky toward your friend, or the table, and then pull it back to its original position. Did you see the wave?
5. Now do it again, back and forth several times and watch where the slinky is bunched up and where it’s spread out.
6. Notice the tape. What is it doing?
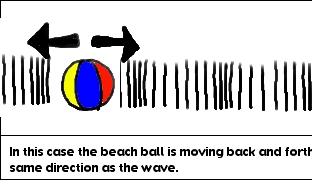Here you made a longitudinal wave. A longitudinal wave is where the particle moves parallel to the medium. In other words, your hand vibrated in the same direction (parallel to the direction) the wave was moving in. Your vibrating hand created a wave that was moving in the same direction as the hand was moving in. Did you take a look at the tape? The tape was moving back and forth in the same direction the wave was going.
Do you see the difference between a transverse wave and a longitudinal wave? In a transverse waves the particles vibrate in a different direction (perpendicular) to the wave. In a longitudinal wave the particles vibrate in the same direction (parallel) to the wave.
What’s the Difference between Amplitude and Wavelength?
Here’s an easy way to get a feel for amplitude:
1. Put a piece of tape in about the middle of the rope.
2. Tie your rope to something or let your friend hold on to one end of it.
3. Now pull the rope so that it is a bit slack but not quite touching the floor.
4. Your friend should hold their hands as still as possible.
5. Vibrate your hand but only move it up and down about a foot or so. Have your partner pay attention to how that feels when the wave hits him or her.
6. Now, vibrate your hand but now move it up and down 2 or 3 feet. How does that feel to your partner?
7. Have your partner do the vibrating now and see what you feel.
You created two different amplitude waves. The first wave had a smaller amplitude than the second wave. What you and your partner should have felt was more energy the second time. The wave should have hit your hand with more energy when the wave had more amplitude.
Here’s a great way to visualize wavelength:
1. Tie your rope to something or let your friend hold on to it.
2. Now pull the rope so that it is a bit slack but not quite touching the floor.
3. Your friend should hold their hands as still as possible.
4. Now begin vibrating your hand fairly slowly. In this case, it works better if you move your hand in a circle.
5. Try to make a wavelength with the rope. In other words it will look like you’re playing jump rope.
6. Now try a one and a half wavelengths.
7. Can you get two or more wavelengths? You’ve really got to get your hand moving to get it.
In this image, the left wave is ONE wavelength, the middle is 1.5 wavelegnths, and the right is TWO wavelengths. See the difference?
Did you notice how the frequency of your hand determined the wavelength of the rope? The faster your hand, moved the more wavelengths you could get.
[/am4show]
Click here to go to next lesson on Motion of Waves.
This is a recording of a recent live teleclass I did with thousands of kids from all over the world. I’ve included it here so you can participate and learn, too!
Sound is a form of energy, and is caused by something vibrating. So what is moving to make sound energy?
Molecules. Molecules are vibrating back and forth at fairly high rates of speed, creating waves. Energy moves from place to place by waves. Sound energy moves by longitudinal waves (the waves that are like a slinky). The molecules vibrate back and forth, crashing into the molecules next to them, causing them to vibrate, and so on and so forth. All sounds come from vibrations.
Materials:
- 1 tongue-depressor size popsicle stick
- Three 3″ x 1/4″ rubber bands
- 2 index cards
- 3 feet of string (or yarn)
- scissors
- tape or hot glue
[am4show have=’p8;p9;p100;’ guest_error=’Guest error message’ user_error=’User error message’ ]
What’s Going On?
Do you remember where all waves come from? Vibrating particles. Waves come from vibrating particles and are made up of vibrating particles.
Here’s rule one when it comes to waves…. the waves move, the particles don’t. The wave moves from place to place. The wave carries the energy from place to place. The particles however, stay put. Here’s a couple of examples to keep in mind.
If you’ve ever seen a crowd of people do the ‘wave’ in the stands of a sporting event you may have noticed that the people only vibrated up and down. They did not move along the wave. The wave, however, moved through the stands.
Another example would be a duck floating on a wavy lake. The duck is moving up and down (vibrating) just like the water particles but he is not moving with the waves. The waves move but the particles don’t. When I talk to you, the vibrating air molecules that made the sound in my mouth do not travel across the room into your ears. (Which is especially handy if I’ve just eaten an onion sandwich!) The energy from my mouth is moved, by waves, across the room.
Questions to Ask
- Does the shape of the index card matter?
- What happens if you change the number of rubber bands?
- What if you use a different thickness rubber band?
- What happens if you make the string longer or shorter?
- can you make a double by stacking two together?
- Can you get a second or third harmonic by swinging it around faster?
- Why do you need the index card at all?
[/am4show]
Click here to go to next lesson on Energy of a Wave.
Since the particles don’t travel with the wave, what does a wave carry? Waves transport energy, not particles (or matter).
[am4show have=’p9;p58;’ guest_error=’Guest error message’ user_error=’User error message’ ]
Click here to go to next lesson on Mechanical and Electromagnetic Waves.
[/am4show]
Some waves need a medium to travel through while others do not. Mechanical waves need a medium for the wave to travel through to transport energy. Ocean waves, jump ropes, pendulums, sound, and waves in a stadium are all examples of mechanical waves.
[am4show have=’p9;p58;’ guest_error=’Guest error message’ user_error=’User error message’ ]
Electromagnetic waves do not need a medium to travel through. Light from the sun reaches up 93 million miles away by traveling though the vacuum of space because it’s an electromagnetic wave. The electromagnetic wave travels through the vacuum of space at the speed of light (299,792,458 m/s). These types of waves are made by vibrating charged particles, and we’re going to look at this more in depth in our next section on Light.
Matter waves are the ones you get to learn about when you study quantum physics, as they describe the way that matter (like a beam of electrons) under certain conditions acts like a wave. That’s way out of our scope here, but I want you to at least be aware that they exist.
Click here to go to next lesson on Properties of a Wave.
[/am4show]
The words particle and wave are two words you’ll see in nearly every area of physics, but they are actually very different from each other. A particle is a tiny concentration of something that can transmit energy, and a wave is a broad distribution of energy that fills the space it passes through. We’re going to look at particles in more depth later, and instead focus on understanding waves.
[am4show have=’p9;p58;’ guest_error=’Guest error message’ user_error=’User error message’ ]
A wave traveling along a stretched string can have different shapes, but every wave will have a frequency and a wavelength. Wavelength refers to the repeating wave shape, and frequency refers to the oscillating source that make the wave in the first place. Waves are defined by a math equation that we’ll get to a little later. First, let’s take a look at the different parts of a wave.
A wave number is the number of waves per unit length.
For longitudinal waves, a rarefaction is the spot where the the wave is traveling and is the most “stretched out” (minimum wave density). The compression is the spot where the wave is most squished together. You can see this easily if you play with a slinky… the coils that are most spread out are a rarefaction point.
Click here to go to next lesson on Period, Frequency, Amplitude and Wavelength.
[/am4show]
A wave can have many different shapes, but it has a very specific frequency ν and wavelength λ.
[am4show have=’p9;p58;’ guest_error=’Guest error message’ user_error=’User error message’ ]
Click here to go to next lesson on Humming Bird.
[/am4show]
Humming birds are really fascinating, because they can beat their wings so fast! Here’s a quick way to calculate the frequency and period of a humming bird’s wings.
[am4show have=’p9;p58;’ guest_error=’Guest error message’ user_error=’User error message’ ]
Click here to go to next lesson on Swinging Kid.
[/am4show]
Kids love swings, and it’s amazingly simple to find the frequency and period of the swing. Here’s how…
[am4show have=’p9;p58;’ guest_error=’Guest error message’ user_error=’User error message’ ]
Click here to go to next lesson on Energy and Wave Amplitude.
[/am4show]
How is the energy related to the wave frequency, amplitude and wavelength?
[am4show have=’p9;p58;’ guest_error=’Guest error message’ user_error=’User error message’ ]
Click here to go to next lesson on Wave Speed.
[/am4show]
Sound is a type of energy, and energy moves by waves. So sound moves from one place to another by waves; longitudinal waves to be more specific. So, how fast do sound waves travel? Well, that’s a bit of a tricky question. The speed of the wave depends on what kind of stuff the wave is moving through. The more dense (thicker) the material, the faster sound can travel through it.
[am4show have=’p9;p58;’ guest_error=’Guest error message’ user_error=’User error message’ ]
Remember that waves move because the particles bounce off one another? Well, the farther the particles are from one another, the longer it takes one particle to bounce off another. Think about a row of dominoes. If you put them all close together and push one over they all fall down pretty quick. If you spread them out a bit, the row falls much more slowly. Sound waves move the same way.
Click here to go to next lesson on More on Wave Speed .
[/am4show]
Sound moves faster in solid objects than it does in air because the molecules are very close together in a solid and very far apart in a gas. For example, sound travels at about 760 mph in air, 3300 mph in water, 11,400 mph in aluminum, and 27,000 mph in diamond!
[am4show have=’p9;p58;’ guest_error=’Guest error message’ user_error=’User error message’ ]
The temperature of the material also makes a difference. The colder the material, the faster the sound. This is why sound seems to be louder or clearer in the winter or at night. The air is a little cooler and since it’s cooler, the molecules are a little more tightly packed.
The speed of a wave is based on the basic distance over time relationship. If you watch the crest of a wave, the speed is how fast the crest is observed to move a distance.
Click here to go to next lesson on Echoes.
[/am4show]
An echo is when a wave travels through one medium (like air) and then meets a different medium (like a cave wall). The sound wave bounces and reflects back to you.
[am4show have=’p9;p58;’ guest_error=’Guest error message’ user_error=’User error message’ ]
Click here to go to next lesson on Bird Waves.
[/am4show]
Let’s do a couple of simpler sample problems, and then I’ll show you how to do problems that are more complex and involve higher level math. First, let’s take a look at the wings of a bird in flight…
[am4show have=’p9;p58;’ guest_error=’Guest error message’ user_error=’User error message’ ]
Click here to go to next lesson on Sitting on the Ocean.
[/am4show]
Ocean waves travel on the surface of the water can be observed and measured. Let’s try one just before a storm…
[am4show have=’p9;p58;’ guest_error=’Guest error message’ user_error=’User error message’ ]
Click here to go to next lesson on Seasick Waves.
[/am4show]
Ever gotten sea sick? It’s usually because the motion of what your body detects is different from what your eyes see. Let’s take a look at how you can calculate the wave speed by watching two boats bobbing up and down (without getting sick).
[am4show have=’p9;p58;’ guest_error=’Guest error message’ user_error=’User error message’ ]
Click here to go to next lesson on Wave Speed on Tight Strings.
[/am4show]
Waves traveling on a tight string, like a climbing rope, are dependent on only two things: the tension of the rope and a physical property of the rope (like what it’s made out of, the diameter, etc.).
[am4show have=’p9;p58;’ guest_error=’Guest error message’ user_error=’User error message’ ]
Click here to go to next lesson on Wave Equations.
[/am4show]
Now it’s time for a little more math because the physics problems are going to get a little harder.
[am4show have=’p9;p58;’ guest_error=’Guest error message’ user_error=’User error message’ ]
The wave equation for transverse and longitudinal waves moving in the +x direction looks like this:
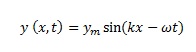
where ym is the amplitude of the wave, κ is the angular wave number, ω is the angular frequency, and (κx-ωt) is the phase.
The wavelength L and the wave number k are found by the following equation:
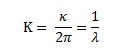
where K is the number of waves per meter.
The period (T) and the frequency (ν) are related to ω by the following equation:
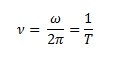
The main wave speed equation is given by:
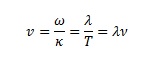
Note that the first letter v is for velocity, and the last letter in the equation is the greek letter “nu” (ν) for frequency.
The problems in the video involve using the first equation that relates the distance and time to find the amplitude, wave number, and frequency of a wave. (This is a typical problem that you’ll see in college level physics.)
Click here to go to next lesson on Waves on a Stretched String.
[/am4show]
If a wave can travel through mediums like air, water, strings, rocks, etc., then it makes sense that as the wave moves through these mediums, the tiny particles that make up the medium will also vibrate. In order for this to happen, the medium has to have a way for energy (both potential and kinetic) to be stored, so the medium has both inertia and elasticity.
[am4show have=’p9;p58;’ guest_error=’Guest error message’ user_error=’User error message’ ]
The wave equation for a stretched spring is:
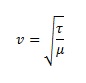
where the first letter v is for velocity, μ is the linear density of the string, and the tension is τ.
You can’t send a wave along a straight string without stretching the string. The tension in the string that does the stretching is the elasticity of the string that stores the potential energy as the wave passes through. The amount of tension in the rope will affect the wave speed. The wave speed doesn’t change if you change the frequency, however it will travel faster through a tighter rope.
This means that the speed of the wave depends on the medium, and not the wave itself. For example, waves travel faster through solid rock than they do through air because the particles in the medium are much closer together and can transmit the wave faster.
Here’s the power part of the video above explained in more detail:
Click here to go to next lesson on Behavior of Waves
[/am4show]