Although the Möbius strip is named for German mathematician August Möbius, it was co-discovered independently by Johann Benedict Listing, a completely different German mathematician, but at around the same time in 1858. Weird, right? But that’s not the only strange thing about the Möbius strip. It’s a non-orientable surface. This means it has a path that will take a traveler back to their point of origin. Are you completely confused now? That’s okay! Just watch the video and I’ll explain.
[am4show have=’p8;p9;p11;p38;p154;’ guest_error=’Guest error message’ user_error=’User error message’ ]
Download Student Worksheet & Exercises
So a paradox is something that seems to contradict itself – it sort of makes sense, but then again it doesn’t really make sense. It seems odd that a paradox fits into a math lesson, yet they do exist in mathematics. The Möbius strip is a fun example of a paradox that you can actually touch. What happens when you cut the Möbius strip like I show in the video?
Exercises
Identify the figures shown below:
1. 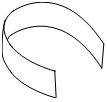 |
2. 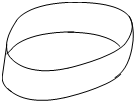 |
3. 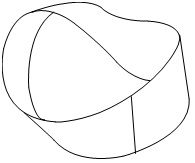 |
4. 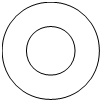 |
- How many faces does a Möbius strip have?
- How many edges does a Möbius strip have?
- Given a strip of paper, at which angle should one rotate one of its ends before connecting to form a Möbius strip?
- When a person cuts along the length of the Möbius strip to come up with a longer one, how many twists does he observe in the final strip?
- Say you want to get two Möbius strips from an existing one. How would you do it?
- If you cut the Möbius strip along its length as shown in 9 above, how many connected strips would you get?
[/am4show]


Isn’t that cool? I Love this experiment!
I cut the strip again after the first cut and I got two strips linked together!!!! 🙂